
64
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. «Естественные науки». 2016. № 3
Введем следующие обозначения:
1
,
m
2
m
— массы мятников;
—
l
длина невесо-
мого стержня
AB
;
,
b
δ
—
расстояния
0
OB
и
0
,
OC
соответствующие
n
-му тону колеба-
ний слоев жидкостей.
Как показывает анализ дифференциаль-
ных уравнений для обобщенных координат
волновых движений по поверхности разделов
трех слоев жидкостей каждому индексу «
n
»
соответствуют два главных колебания, часто-
ты которых могут быть определены по фор-
мулам (17)–(19). Следовательно, для каждого
индекса «
n
» механической модели должны
возникать два главных колебания, т. е. экви-
валентный механический аналог колебаний
поверхностей разделов слоев жидкостей должен иметь две степени сво-
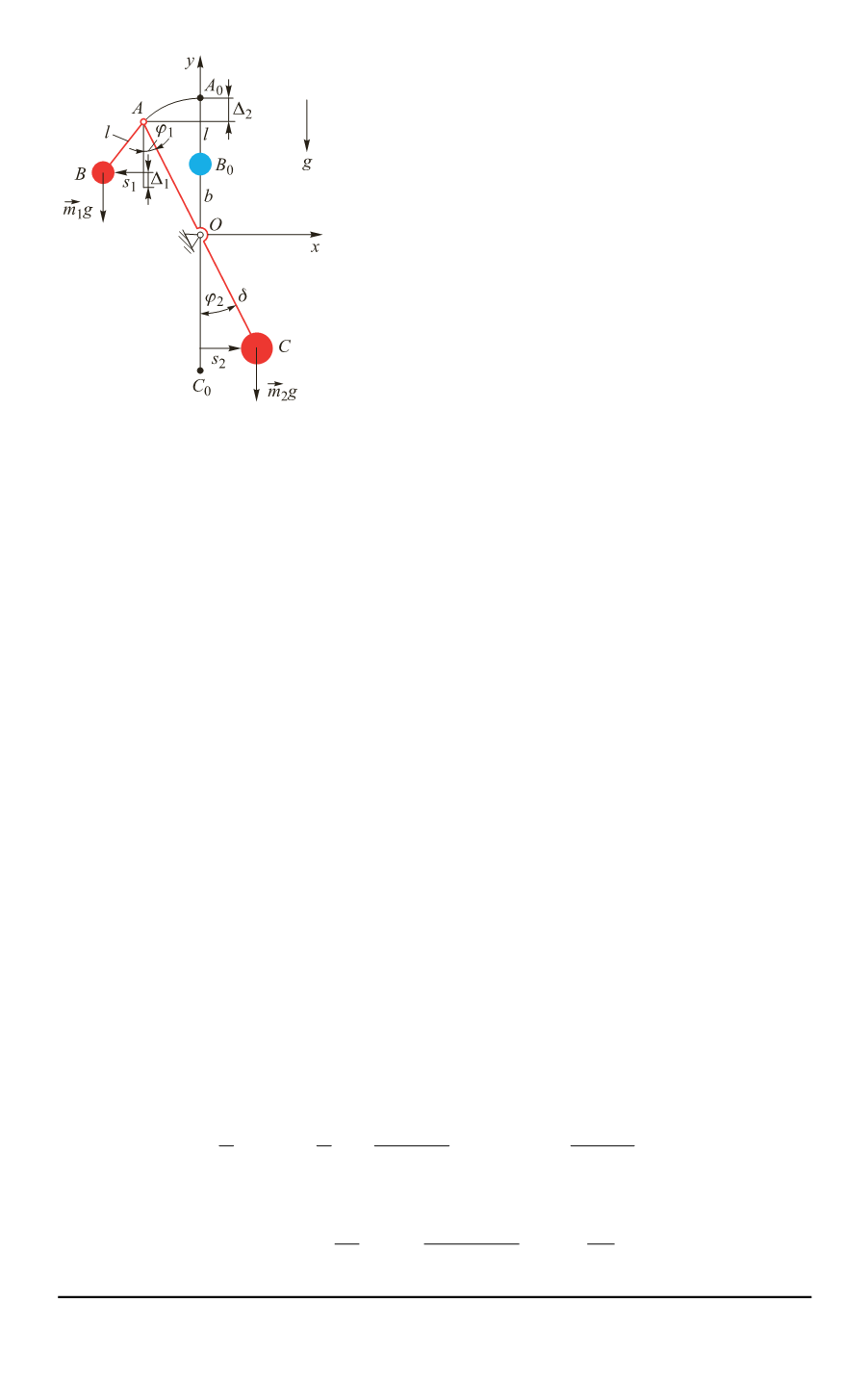
боды. Покажем, что для предлагаемого механического аналога (см.
рис. 5) уравнения движения будут совпадать с уравнениями для обоб-
щенных координат
1
n
t
и
2
.
n
t
Составим выражения для кинетической и потенциальной энергий
предлагаемой механической системы. За обобщенные координаты
примем расстояния
1 2
, ,
s s
определяющие положение маятника массой
2
m
(точка
C
) и положение маятника массой
1
m
(точка
B
) (см. рис. 5).
Координаты точек
C
и
B
в системе координат
xOy
будут
2
sin ;
С
x
2
co ; s
С
y
2
1
sin
sin
В
x
l b
l
;
2
1
cos
cos .
В
y
l b
l
Кинетическая и потенциальная энергия рассматриваемой механи-
ческой системы с точностью до величин второго порядка малости бу-
дет включать в себя кинетическую и потенциальную энергию маятни-
ков
2
2
2 2
2 2
1
2
1
1 2
2
1
1
2
2
2
l b
l b
T m s
m
s s
s s
;
2
2
2
1
2
1
2
1
1
2
2
П
2
2
2
l b s
s
s
m g m g
m g
l
.
Рис. 5.
Механическая
модель
















