
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. «Естественные науки». 2016. № 3
65
Далее воспользуемся уравнениями Лагранжа второго рода и запи-
шем уравнения колебаний системы маятников
1 1 1 1 1
2
2
2 1
2
2 1
2 1
1
2
0;
0.
l b
g
m s m s m s
l
l b
l b
l b
g
m m
s
m m
s m s
(20)
Сопоставив уравнения колебаний жидкости (15) и уравнения коле-
бания механического аналога (20), определим параметры предлагаемой
маятниковой системы. Сравнив уравнения движения, получим, что
рассматриваемые механические системы будут эквивалентны при
условии равенства обобщенных координат
in
и
s ,
k
,
1, 2,
i k
если
параметры механического аналога будут определены по следующим
формулам:
1
0 0
;
n
n n
m m f m
1
1
;
ch
n
n
m b
l
m k h
2
1
2
1
ch
δ
;
n
n
n n n
m m k h
g
m m
2
2
1
2
1
1
;
ch
n
n n
n
n
m
m m f
m
m k h
1
0
1
.
th
n
n n n
m
l
m m k k h
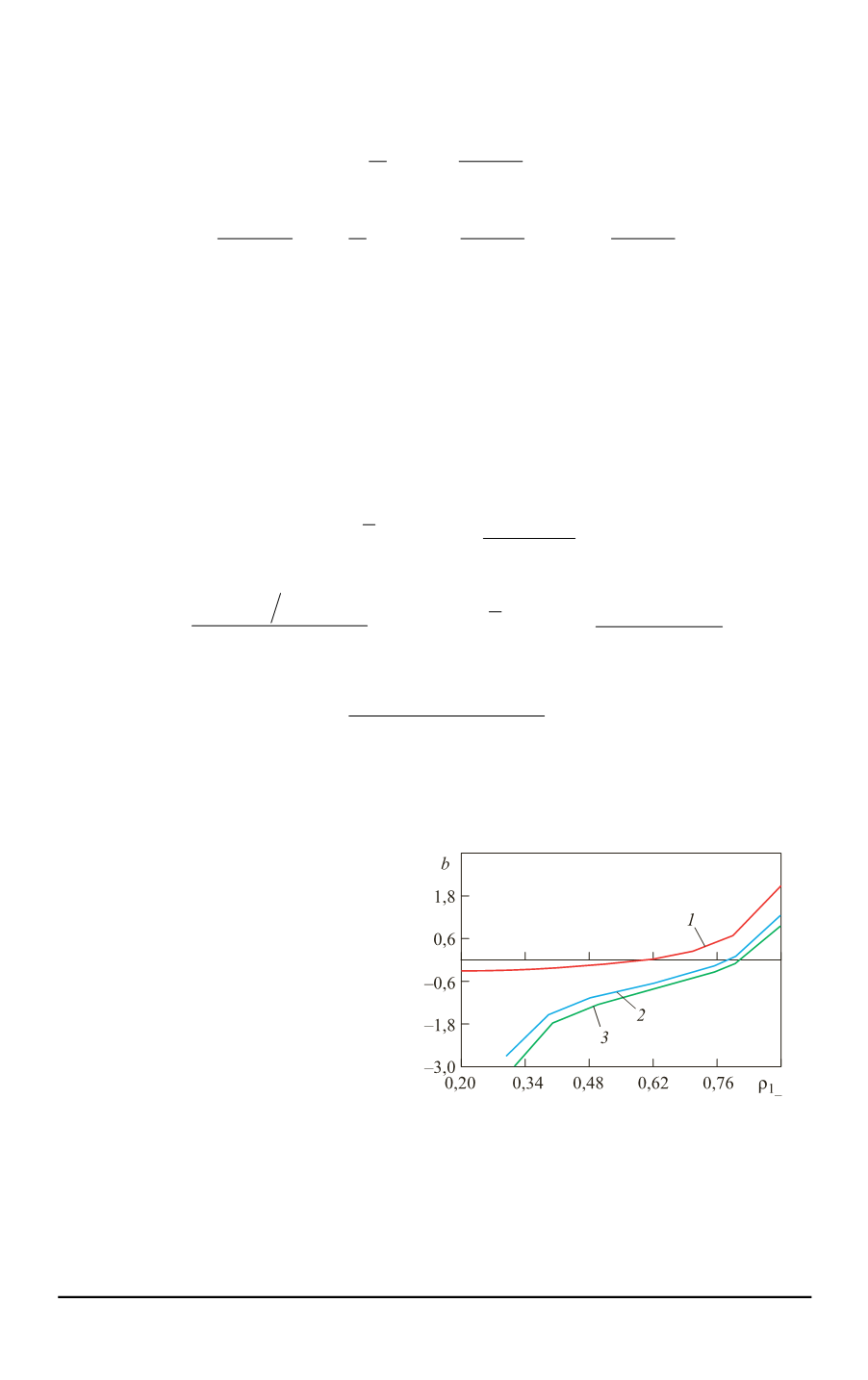
Зависимость расстояния
b
от относительных плотностей жидкостей
1
(
1,8412)
приведена на рис. 6.
Маятниковые аналоги колебаний слоев жидкости при
b
> 0 и
b
< 0
представлены на рис. 7,
а
,
б
, маятниковый аналог колебаний двух сло-
ев жидкости, полностью заполняющих цилиндрический бак, —
на рис. 7,
в
.
Рис. 6.
Зависимость расстояния
b
от относительной плотности
1_
ρ
при
0 _
ρ
= 0 (
1
),
1_
= 0,2 (
2
)
и
2 _
= 0,3 (
3
)
















