
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. «Естественные науки». 2016. № 3
77
,
[0, *
( ) = max |
( ) | |
min,
]
x
t
t
J
n t
(22)
где
— множество, заданное допустимыми значениями параметров
0
0 *
*
= ( ,
,
,
,
,
).
Для решения оптимизационной задачи при
наличии ограничений использована стандартная функция среды
fmincon. В качестве алгоритма численного решения задачи применен
алгоритм Interior Point [15–17]. Отметим, что при нахождении про-
граммных управлений согласно (11) необходимости в вычислении
sin
и
cos
через функции
L
и
H
в процессе моделирования нет, по-
скольку при интегрировании исходной системы (1) рассчитывается те-
кущее значение угла
.
При моделировании использованы граничные условия
*
*
*
*
*
(0) = 1000 м, (0) = 0 м,
( ) = 100 м,
( ) = 20000 м,
(0) = 3 м/с, (0) = 90 м/с,
( ) = 1 м/с, ( ) = 61 м/с,
= 300 с
H
L
H t
L t
H
L
H t
L t
t
и ограничения на переменные состояния
( ) = 0,5 м/с,
( ) = 4,5 м/с,
( ) = 200 / 3,6 м/с,
( ) = 700 / 3,6 м/с.
H H
H H
L L
L L
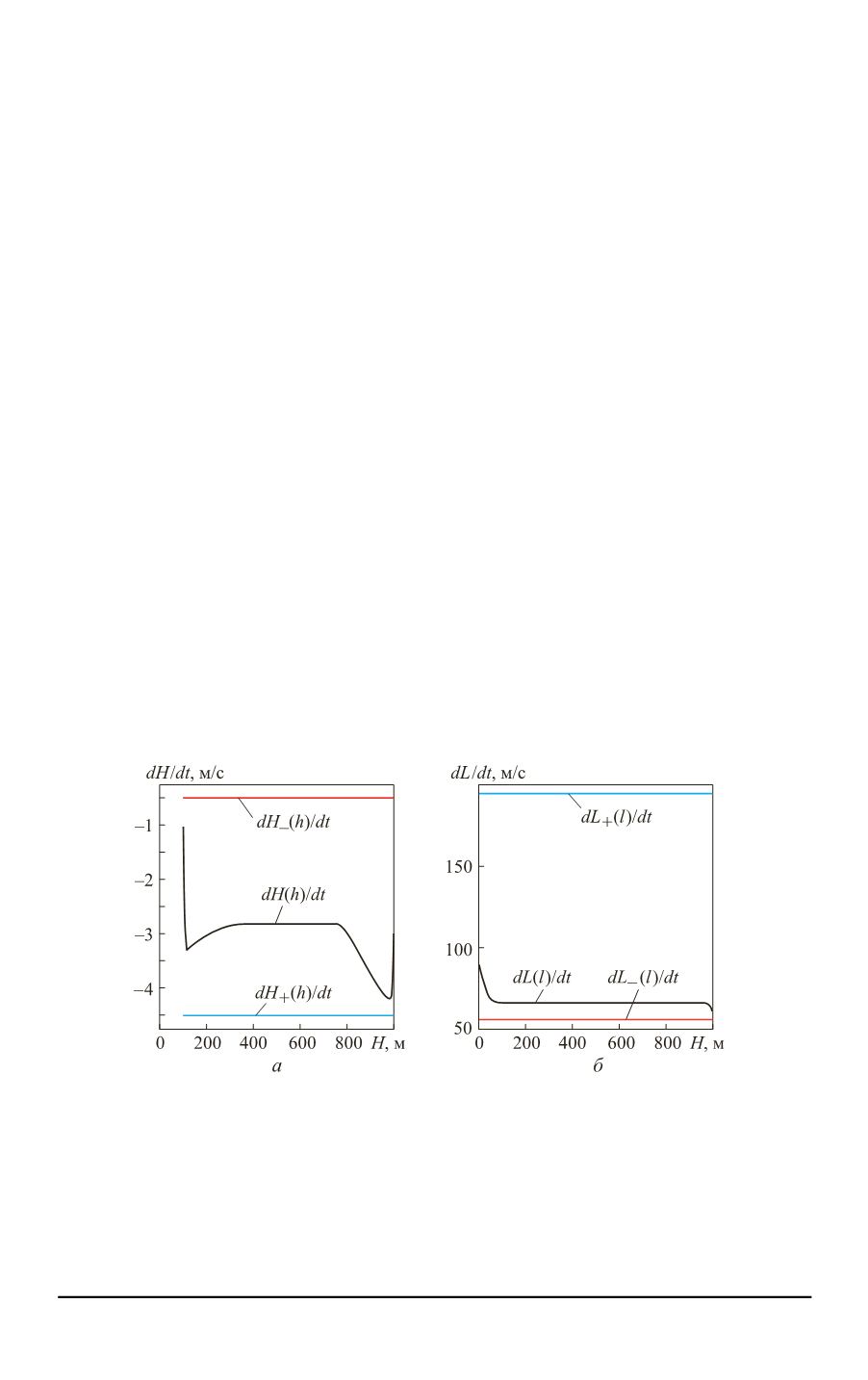
Фазовые траектории по переменным состояния с учетом наложенных
на них ограничений, построенные с помощью метода, приведенного
в работах [10, 11], представлены на рис. 1.
Рис. 1.
Фазовые траектории по высоте (
а
) и по дальности (
б
),
а также ограничения на них
Зависимость высоты от дальности до и после оптимизации показа-
на на рис. 2,
а
, зависимости программных управлений от времени,
полученные до и после решения оптимизационной задачи (22), — на
рис. 2,
б
,
в
.
















