
78
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. «Естественные науки». 2016. № 3
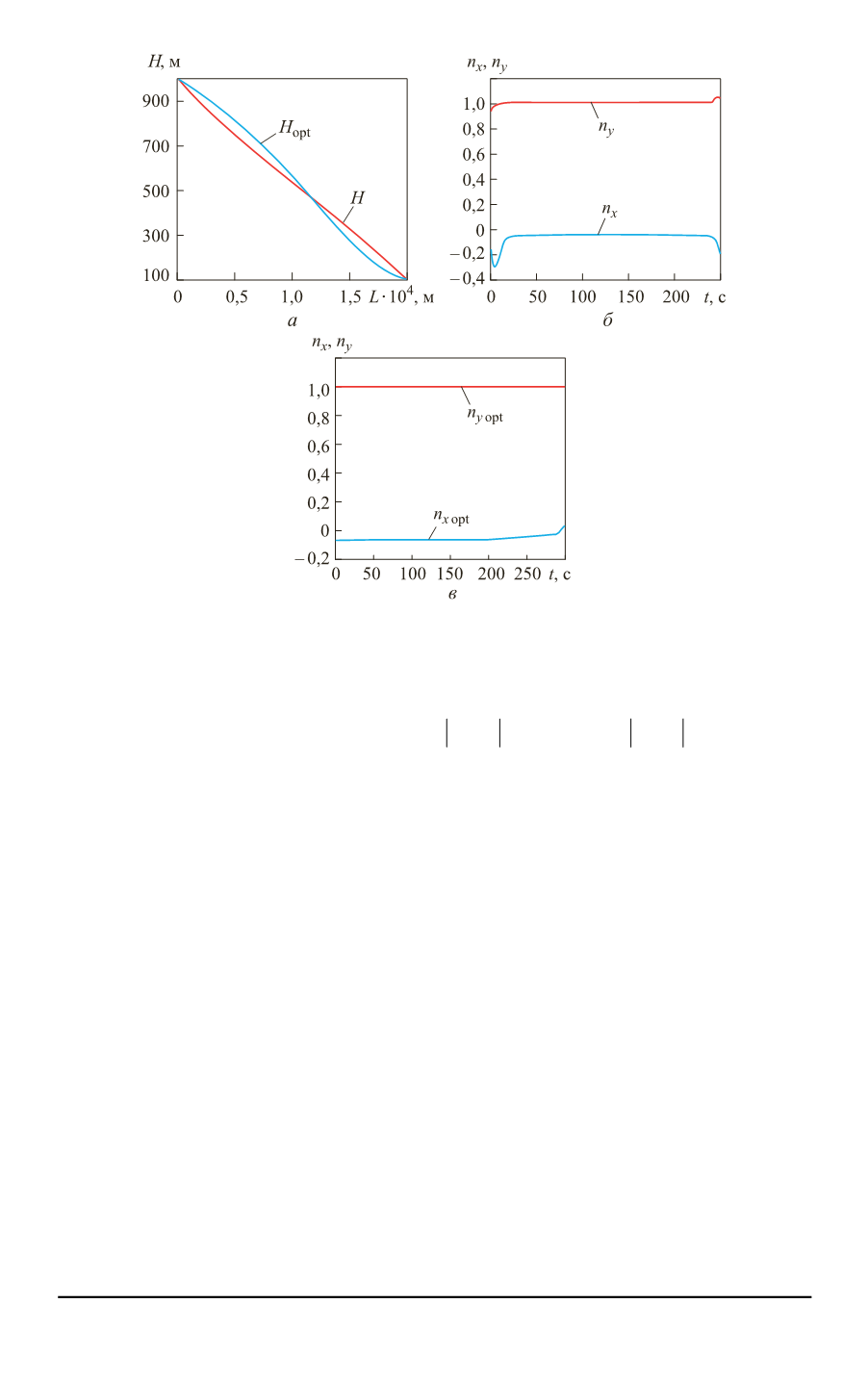
Рис. 2.
Зависимости высоты от дальности до и после оптимизации (
а
),
программных управлений от времени до (
б
) и после (
в
) оптимизации
В результате решения задачи (22) абсолютное максимальное значение
управления
x
n
удалось уменьшить с
( ) = 0, 285
x
n t
до
( ) = 0, 07,
x
n t
что
соответствует снижению целевого критерия (22) в 4 раза.
Заключение.
Рассмотрена задача автоматической прокладки тра-
ектории ЛА в вертикальной плоскости при наличии ограничений на
скорость снижения и на линейную скорость ЛА. Предложенный метод
гарантирует, что при реализации программного движении ЛА будут
выполнены все наложенные на переменные состояния ограничения.
При этом построение программной траектории не требует больших
вычислительных затрат, а указанный метод работает при различных
видах ограничений на переменные состояния. Наличие параметриче-
ского семейства функций, являющихся решением поставленной зада-
чи, позволяет рассматривать вопрос об улучшении тех или иных
свойств получаемой программной траектории. Приведены расчетные
формулы для вычисления программного и стабилизирующего управ-
лений, а также результаты численного моделирования, подтверждаю-
щие работоспособность предложенного метода.
Работа выполнена при финансовой поддержке РФФИ (гранты
№ 14-01-00424 и № 15-07-06484) и Минобрнауки РФ (проект 1.644.2014/К).
















