Расчетыдля наномеди.
С использованием размерной зависимости
температуры плавления, полученной в [9] методом молекулярной ди-
намики для ГЦК-меди (
k
n
(
N
=
∞
) = 12
;
k
p
= 0
,
7405
;
α
= 0
,
7071
), и
выражения (12) для величины функции формы было получено (рис. 1)
Z
s
(
s
) = 2
. Так как нанокапля имеет энергетически наиболее выгодную
форму сферы, для оценки зависимости
k
n
(
l
)
∗
примем
Z
s
(
l
)
= 1. Таким
образом, для проверки обоснованности зависимостей (10) и (13) ис-
пользуем для температуры плавления нанокристалла и температуры
начала кристаллизации нанокапли зависимости, показанные на рис. 1,
T
∗
m
∼
=
k
n
(
s
)
∗
∼
= 1
−
2
·
0
,
7937
1
N
1
/
3
,
T
∗
N
∼
=
k
n
(
l
)
∗
∼
= 1
−
0
,
7937
1
N
1
/
3
.
(17)
Значение скрытой теплоты плавления и температуры плавления ма-
крокристалла меди составляют [9]:
Δ
h
(
N
=
∞
) = 13
,
02
кДж/моль и
T
m
(
N
=
∞
) = 1356
K. Отсюда для скачка удельной энтропии ФПК-Ж
имеем
Δ
s
m
/k
b
= 1
,
155
. Подставляя это значение
Δ
s
m
/k
b
и формулы
(17) в (10) и (13), получаем зависимости
Δ
s
(
N
)
∗
и
Δ
h
(
N
)
∗
, показан-
ные на рис. 1, из которого следует, что функции
Δ
s
∗
и
Δ
h
∗
становятся
равными нулю при
N
−
1
/
3
0
= 0
,
26474026
, т.е. при
INT
(
N
0
) = 54
. Здесь
функция
INT
(
X
) округляет
X
до целого значения, так как
N
— вели-
чина целочисленная.
Известно, что температура кристаллизации макрокристалла всегда
меньше его температуры плавления, причем для меди имеем оцен-
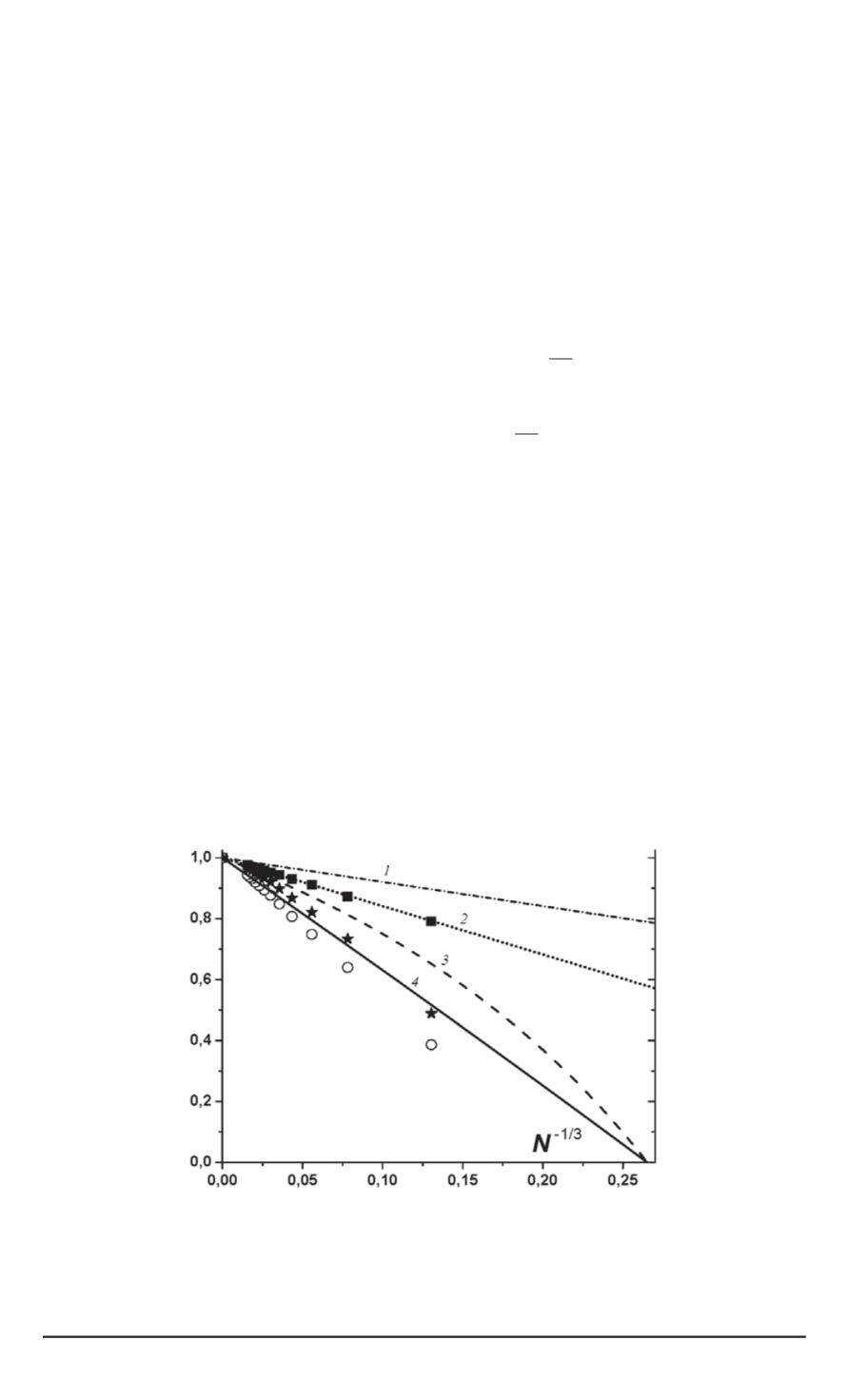
Рис. 1. Зависимость относительных температуры плавления ( и . . . . . . ), скач-
ка энтропии ( и – – –) и скрытой теплоты (
◦
и ———) ФПК-Ж от
N
−
1
/
3
для
наномеди (символы— результаты[9], линии — полученные зависимости):
1
и
2
— расчет
T
∗
N
и
T
∗
m
по (17);
3
и
4
— расчет
Δ
s
∗
и
δh
∗
по (10) и (13) при
Δ
s
m
/
k
B
= 1
,
155
42
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2012. № 1


