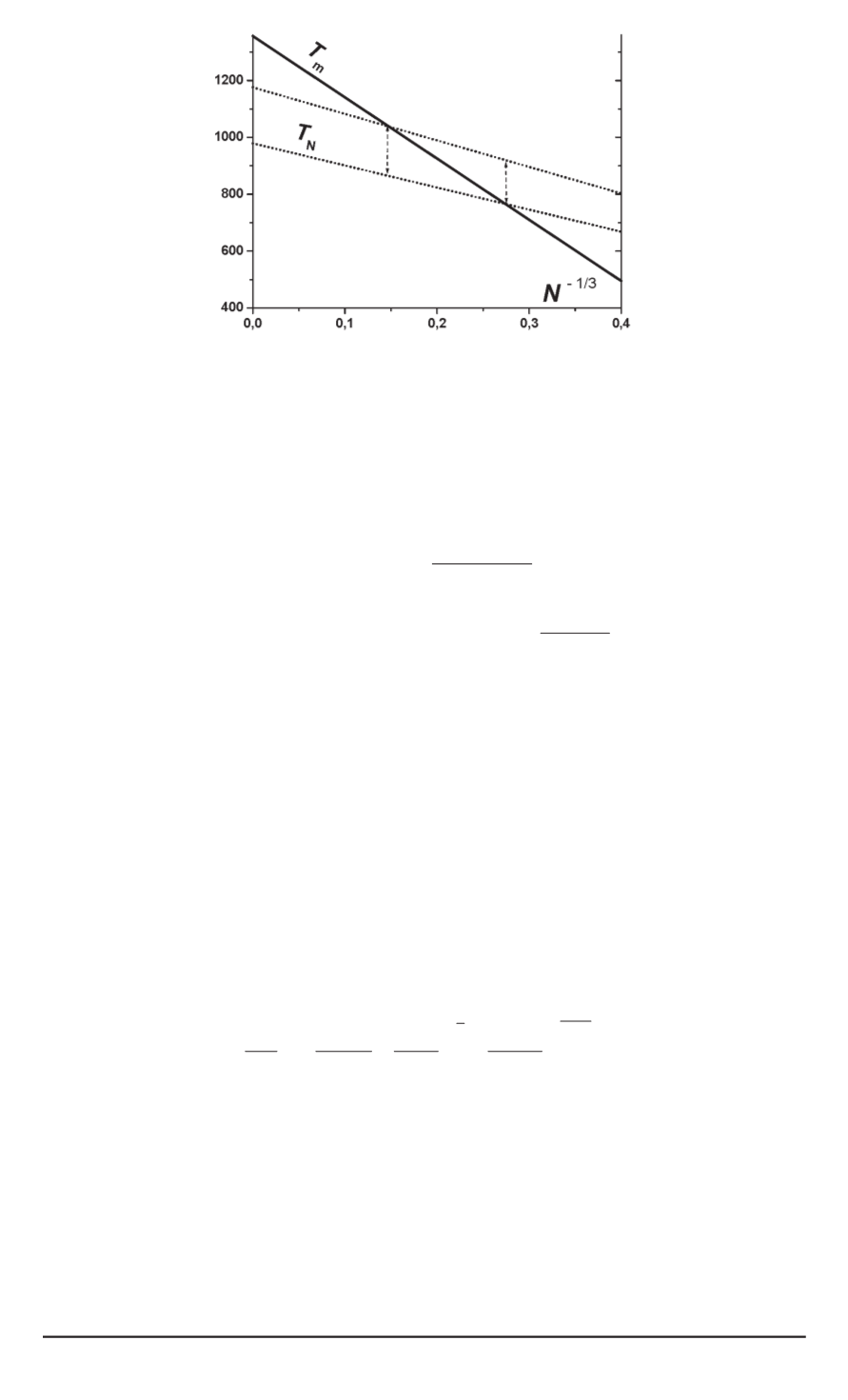
Рис. 2. Зависимости температурыплавления
T
m
(сплошная) и температуры
начала кристаллизации
T
N
(пунктир) от аргумента
N
-1/3
для наномеди
ку [7, 8]
T
N
(
N
=
∞
)
/T
m
(
N
=
∞
) = 0
,
722
. . .
0
,
867
. Используя дан-
ный экспериментальный факт и формулы (17), получим зависимости
(в кельвинах, рис. 2)
T
m
(
N
)
∼
= 1356 1
−
2
·
0
,
7937
N
1
/
3
,
T
N
(
N
)
∼
= (979
. . .
1176)
·
1
−
0
,
7937
N
1
/
3
,
(18)
пересекающиеся при
INT
(
N
x
) = 49
. . .
309
, что дает среднее значение
179. Это хорошо согласуется с результатами, полученными в [2] ме-
тодом молекулярной динамики с использованием потенциала сильной
связи,
INT
(
N
x
) = 125
. . .
135
. Отметим, что в [2] изучалась кристалли-
зация нанокапли меди в нанокристалл с икосаэдрической структурой,
так как методом молекулярной динамики не удалось кристаллизовать
нанокаплю меди сразу в ГЦК-структуру.
Будут ли равны величины
N
x
и
N
0
? Для ответа на этот вопрос
используем локализационный критерий ФПК-Ж [7, 8], исходя из ко-
торого было получено соотношение
T
m
T
N
∼
=
k
n
(
s
)
k
n
(
l
)
v
(
l
)
v
(
s
)
b
3
k
p
(
l
)
k
p
(
s
)
b
+2
3
.
(19)
Здесь
b
— степень отталкивательной ветви парного потенциала меж-
атомного взаимодействия типа Ми–Леннарда–Джонса:
ϕ
(
r
) =
= [
D/
(
b
−
a
)][
a
(
r
o
/r
)
b
−
b
(
r
o
/r
)
a
], который не меняется при
ФПК-Ж и не зависит от размера наночастицы.
В[10] было показано, что если параметр Линдеманна не меняется
с размером нанокристалла, то локализационный критерий ФПК-Ж не
зависит от размера наночастицы. Поэтому если принять
N
x
=
N
0
, то
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2012. № 1
43


