Автомодельное решение задачи теплопереноса в твердом теле, содержащем сферический очаг разогрева с теплопоглощающим покрытием

Автомодельное решение задачи теплопереноса в твердом теле…

ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2016. № 4

103

термически тонком покрытии безразмерная температура очага разогрева со-

ставляет





2 2

   

, т. е. реализуется граничный режим с обострением [14].

Парадоксальность его свойств обусловлена тем, что, несмотря на проявление

эффектов теплопроводности теплота, сосредоточенная в сферическом очаге

разогрева, не распространяется в «холодное» изотропное пространство в тече-

ние всего времени существования режима.

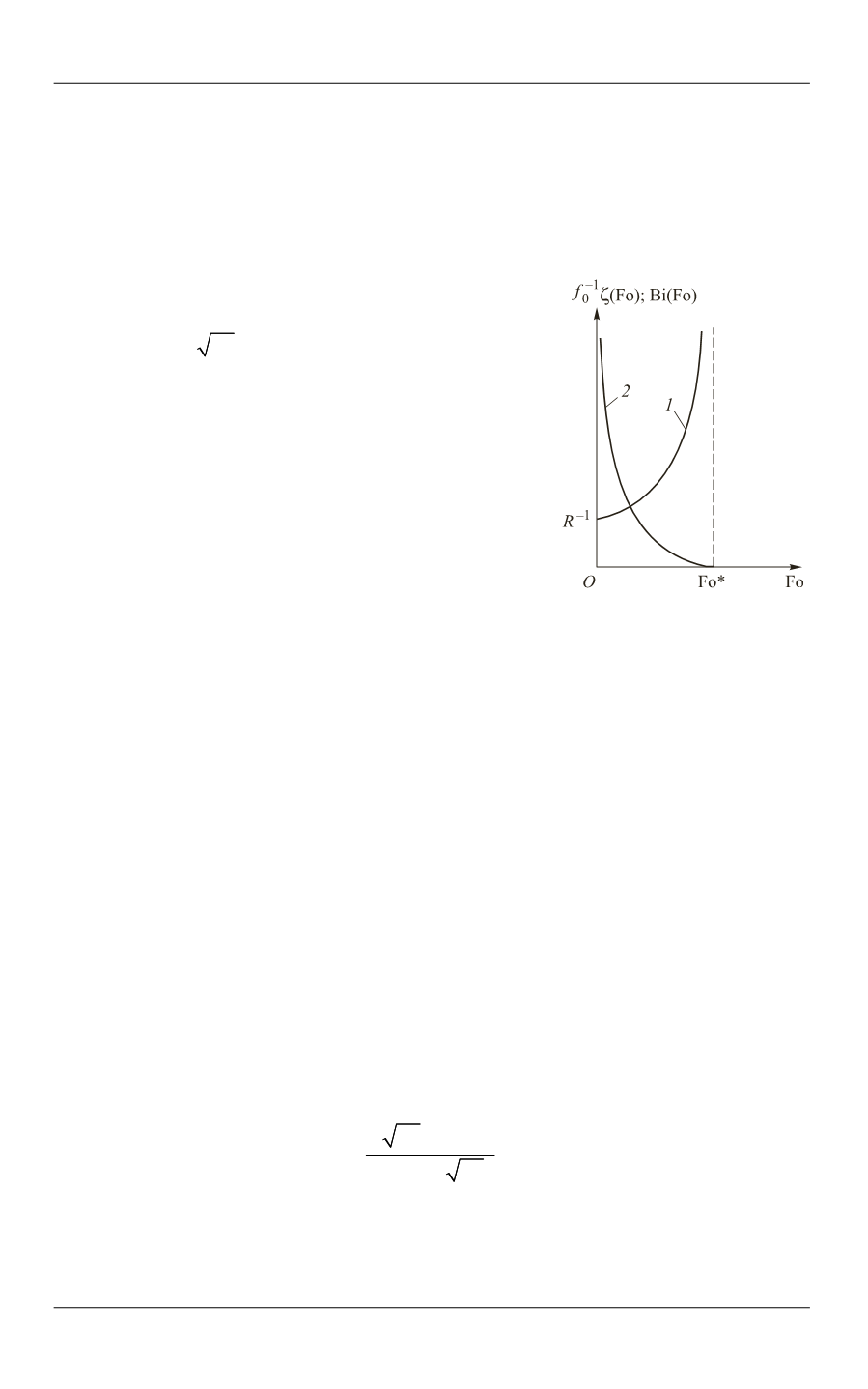
При реализации граничного режима, достаточ-

ное условие автомодельности которого определено

неравенством

Fo ,

 

функция

Bi(Fo),

опреде-

ляющая закон теплообмена в изучаемой системе,

монотонно убывающая, причем

 

Bi(0)

и об-

ращается в нуль в конечный момент времени





 

Функция

 

Bi Fo

называется момен-

том обострения граничного режима, так как

 



 

(рисунок).

Результаты проведенных исследований теорети-

чески обосновывают возможность реализации режи-

ма термостатирования границы сферического очага

разогрева с термически тонким теплопоглощающим

покрытием постоянной толщиной. Безразмерную

температуру границы очага разогрева



(0)





 



, Fo const

R R

определяют по равенству (20),

она зависит от параметра автомодельности

задаваемого условием (17).

Особый интерес представляет случай



наиболее содержательно от-

ражающий специфические особенности автомодельного процесса теплоперено-

са в изучаемой системе. Воспользовавшись равенством (21) при



получим

следующее представление зависимости функций

   

 

Bi Fo ,

Fo и



   

 

Fo Bi Fo

Fo , Fo 0.







Таким образом, закон «компенсирующего» теп-

лопоглощения в термически тонком покрытии

 

Fo ,

обеспечивающий тер-

мостатирование границы очага разогрева, определяется не только реализуемым

режимом теплообмена

 

Bi Fo

в изучаемой системе, но и зависит от закона из-

менения безразмерной температуры

 

Fo .



При этом согласно равенству (23)

при



имеем

 





Fo Fo

, Fo 0,

R R

 



 

а безразмерная температура границы сферического очага разогрева равна





(0)

, Fo 0, Fo 0.

U R R

 

 

Законы изменения безраз-

мерной температуры сфе-

рического очага разогрева

(при

 

Fo 0)

 

и теплооб-

мена в изучаемой системе