
В.Д. Сулимов, П.М. Шкапов, А.В. Сулимов
58
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2016. № 5
В состав алгоритма M-PCALMSI также входят стандартные процедуры Per-
turbation( ) и Small_Perturbation( ) [21]. Гибридные алгоритмы с локальным по-
иском методом сглаживающих аппроксимаций, структурно близкие к описан-
ному алгоритму, представлены в работе [30].
Второй гибридный алгоритм M-PCASFCE объединяет стохастический алго-
ритм M-PCA и алгоритм SFCE, реализующий модифицированный метод кри-
вой, заполняющей пространство (локальный поиск с итеративным оценивани-
ем липшицевых и гельдеровых констант). Выбранный метод локального поиска
обеспечивает сжатие пространства переменных, сканируемого с использовани-
ем стохастического алгоритма, что повышает результирующую вычислительную
эффективность алгоритма M-PCASFCE.
Разработано прикладное программное обеспечение, реализующее новые ги-
бридные алгоритмы M-PCALMSI и M-PCASFCE.
Пример 1.
Рассмотрим прямоугольную матрицу
( )
A x
размером
3 2
со
столбцами
т
1
(1, 1, 1)
A
и
т
2
1
2
( , 0, ) ;
A x x
здесь
R :
,
;
n
j
j
j
D x
a x b j J
2;
n
0, 5;
j
a
1, 5;
j
b
{ 1, 2}.
J
Требуется определить такое решение
*
,
x
при
котором второе сингулярное число матрицы
*
( )
A x
достигает минимума:
найти
2
R
min ( ),
x X
f x
2
( )
( ).
f x
x
Задача имеет точное решение
*
( ) 0,
f x
*
т
(0, 0) ,
x
причем в точке минимума
критериальная функция дифференцируема только по направлениям. Приближен-
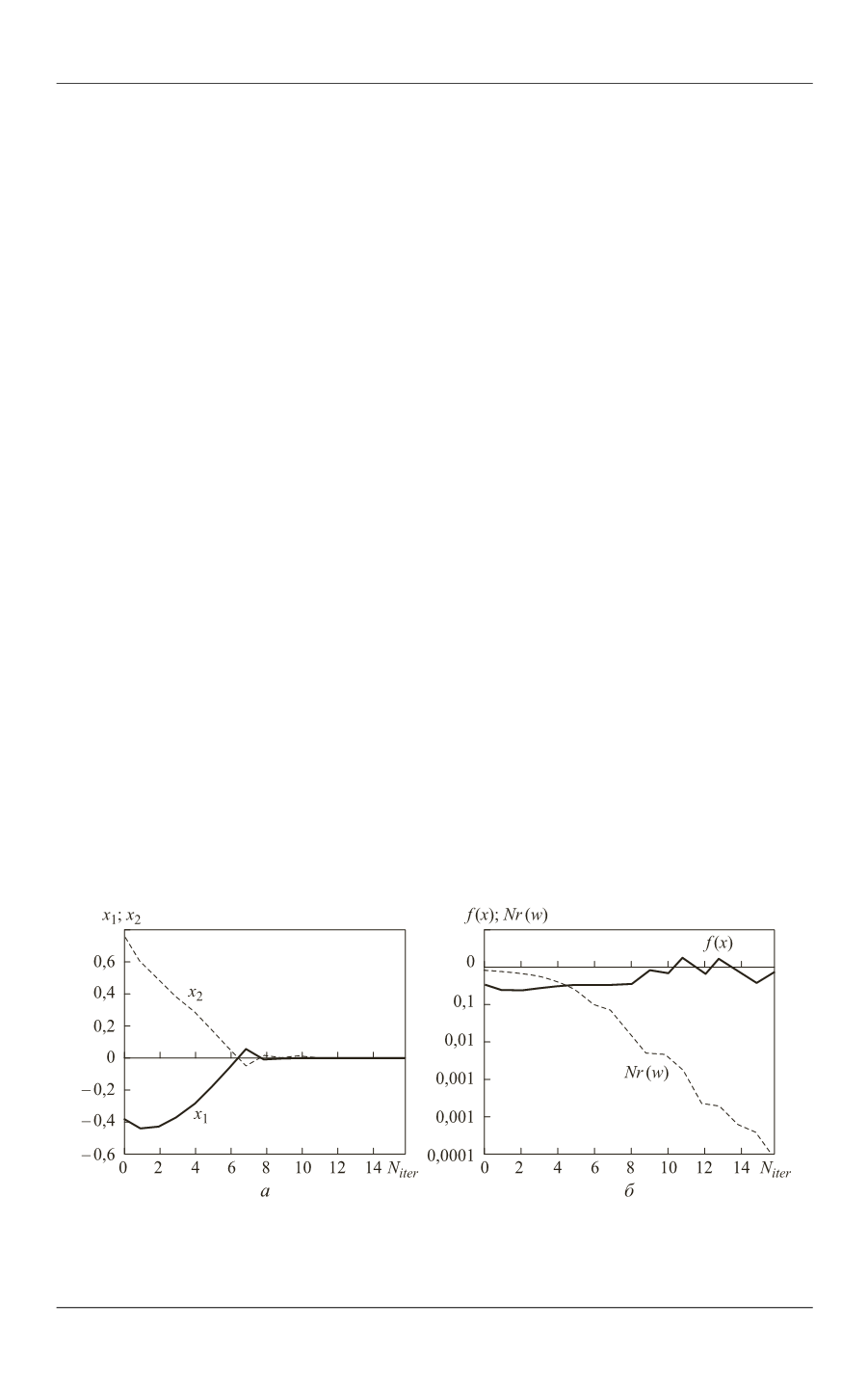
ное решение получено с использованием алгоритма M-PCALMSI. Зависимость пе-
ременных управления
1
,
x
2
,
x
критериальной функции
( )
f x
и нормы
( )
Nr w
век-
тора улучшающего направления от числа итераций в заключительной фазе локаль-
ного поиска, определяющей глобальное решение, приведена на рис. 1.
Рис. 1.
Зависимость переменных управления
1
,
x
2
x
(
а
), функции ( )
f x
и нормы
( )
Nr w
(
б
) вектора улучшающего направления от числа итераций в заключительной фазе
локального поиска
















