уравнений равновесия (1) и соотношений упругости (17) в виде
dT
r
dr
0
=
μ
⎛
⎜⎜⎜⎝
dr
dr
0
−
1
r
−
dr
dr
0
r
2
0
r
3
⎞
⎟⎟⎟⎠
,
dr
dr
0
=
r
0
r
1 +
T
r
K
−
μ
2
K
r
r
0
−
2
−
dr
dr
0
−
2
.
(18)
Для вычисления радиуса поры необходимо проинтегрировать си-
стему уравнений (18) с начальными условиями
T
r
(
r
01
) =
T
1
;
r
(
r
01
) =
r
1
,
(19)
где значение
r
1
выбирается таким, чтобы
T
r
(
r
02
) =
T
1
. Решение си-
стемы нелинейных дифференциальных уравнений (18) с начальными
условиями (19) получено с использованием программного комплек-
са Маple и экспериментальных данных работы [1]:
r
01
= 0
,
002
мкм,
μ
= 0
,
007
дин/см,
K
= 150
дин/см,
T
1
= 6
дин/см. Результаты расчета
приведены в таблице и на рис. 7.
Из таблицы (случай
α
= 0
) и рис. 7 следует, что решения систем
уравнений (14) и (18) практически совпадают для случая бесконеч-
ной области. Таким образом, учет слагаемого
˘
T
=
Kα
в выражениях
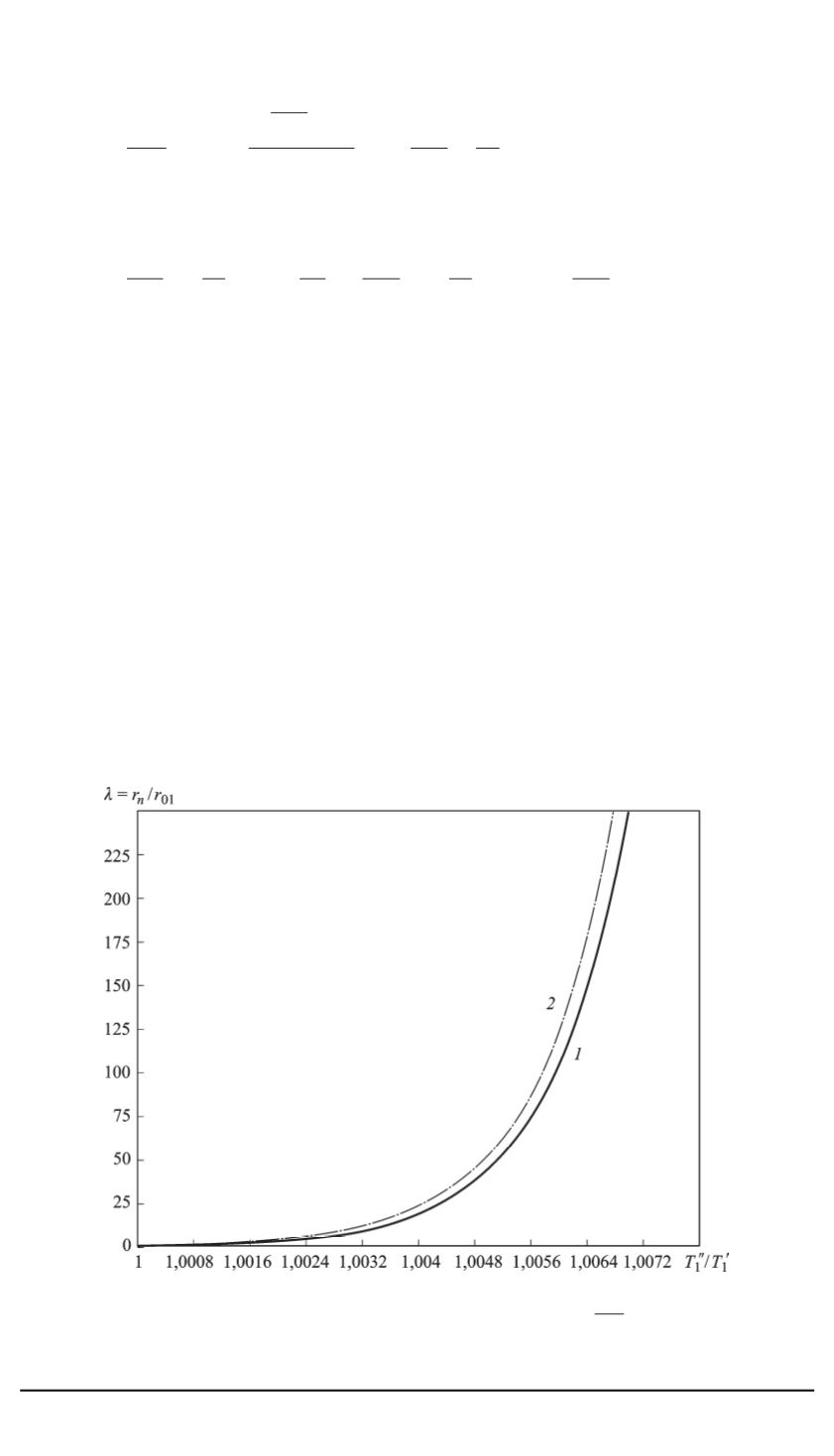
Рис. 7. Зависимости относительного радиуса поры
λ
T
1
T
1
, полученные из
систем уравнений (14) (
α
= 0
, кривая
1
) и(18) (
α
= 0
, кривая
2
)
96
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2012. № 2


