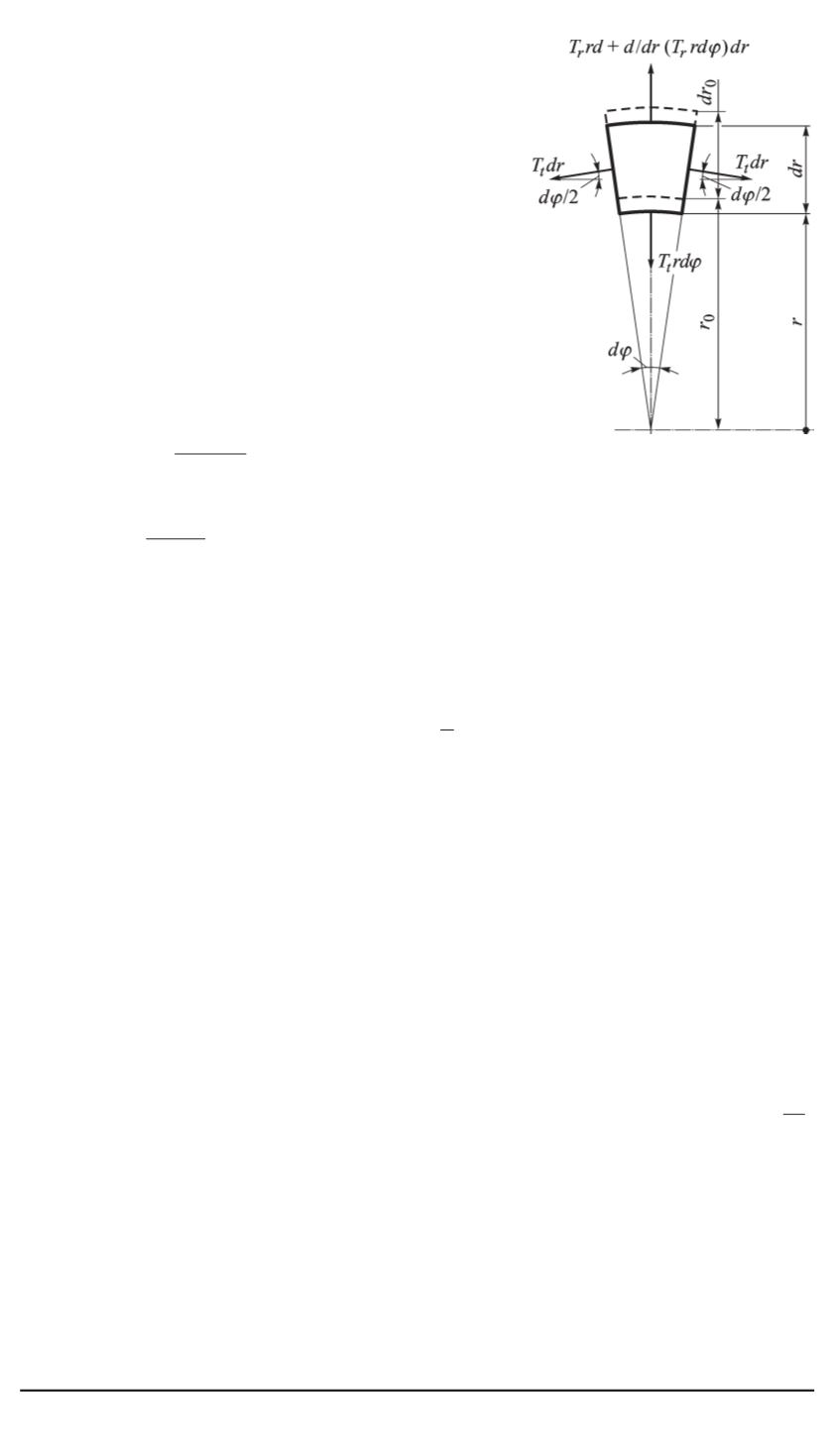
Рис. 4. Расчетная схема эле-
мента поверхности
половине толщины бислоя
h/
2
:
r
п
=
r
1
−
h/
2
.
Для определения радиуса
r
1
рассмотрим
плоскую часть липидной мембраны. Со-
ставим уравнение равновесия для элемен-
та, вырезанного радиальными и окружны-
ми сечениями области вокруг поры (рис. 4),
в актуальном (деформированном) состоя-
нии.
Проектируя силы на радиальное напра-
вление, получим
d
(
T
r
r
)
dr
−
T
t
= 0
,
или
d
(
T
r
)
dr
r
+
T
r
−
T
t
= 0
.
(1)
Чтобы определить зависимость деформации поры от натяжения
воспользуемся соотношениями упругости, полученными в работе [1]
методами термомеханики, на основе выражения для плотности упру-
гой энергии в виде
F
=
μβ
+
1
2
Kα
2
.
(2)
Две функции
α
и
β
полностью характеризуют геометрическую при-
роду деформации:
α
— относительное изменение площади элемента
поверхности, а
β
— относительное изменение формы элемента (длин
сторон). Как было сказано ранее, деформация
α
незначительна, поэто-
му рассмотрим два варианта расчета: первый, когда
α
= 0
и второй —
с учетом второго слагаемого в уравнении (2).
Тела, у которых
F
пропорциональна первой степени параметра
β
, — гиперупругие, поэтому для вывода соотношений упругости при-
менимы методы нелинейной механики. Деформации в таких случаях
описываются степенями удлинения
λ
, которое равно отношению от-
резка после деформации к его первоначальной длине
0
, т.е.
λ
=
0
.
Вывод соотношений упругости из выражения (2) методом нели-
нейной теории упругости [5] для гиперупругого тела с несжимаемым
объемом, дает те же соотношения упругости, что и полученные мето-
дами термомеханики в работе [1].
Вычисление радиуса поры в липидной мембране в случае неиз-
менной площадидеформаци (
F
=
μβ
).
Рассмотрим малый элемент
пластинки единичной длины. Предположим, что толщина мембраны
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2012. № 2
91


