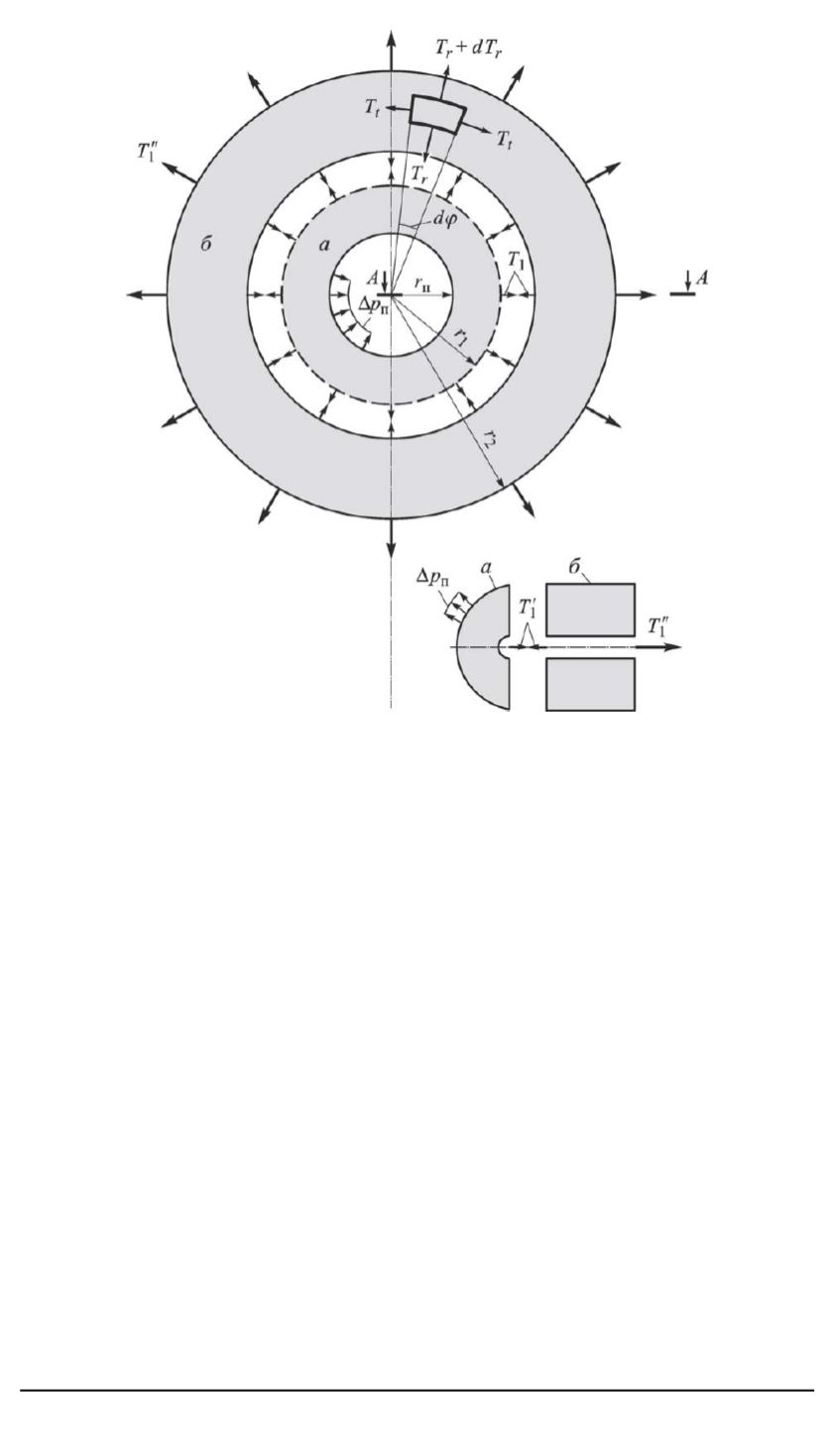
Рис. 2. Схема расчета поры по методу сечений:
а
— область мембраны, образующая торообразную поверхность поры, на которую
действует давление;
б
— область плоской мембраны;
r
п
— радиус поры;
r
1
—
радиус внутренней области мембраны (стыковочный);
r
2
— радиус внешней
области поры;
h
— толщина липидного бислоя;
T
r
— радиальное натяжение;
T
t
—
окружное натяжение;
Т
1
— натяжение мембраны (радиальное);
T
1
— поверхностное
натяжение внутри поры (радиальное)
(состоящего из двух слоев липидов), который далее представлен как
однослойная пластина толщиной
h
. На поверхность тора действует
межфазная разность давлений
Δ
p
п
, которая вызывает натяжение
T
1
и
далее не изменяется. К внешней области радиусом
r
02
, определяемом
экспериментально, приложено натяжение
Т
1
. Поверхность липидно-
го слоя практически нерастяжима, так как жесткость на растяжение
бислоя намного больше жесткости на сдвиг. Благодаря этому расчет
торообразной части упрощается в предположении, что
Δ
p
п
и, соответ-
ственно,
T
1
практически постоянны по величине в процессе деформи-
рования.
Силы в нагруженной постоянным давлением торовой оболочке
(рис. 3,
а
) могут быть рассчитаны на основе безмоментной теории [4].
Сила
Т
1
в одном липидном слое может быть найдена из условия рав-
новесия — равенства суммы проекций на ось симметрии сил, прило-
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2012. № 2
89


