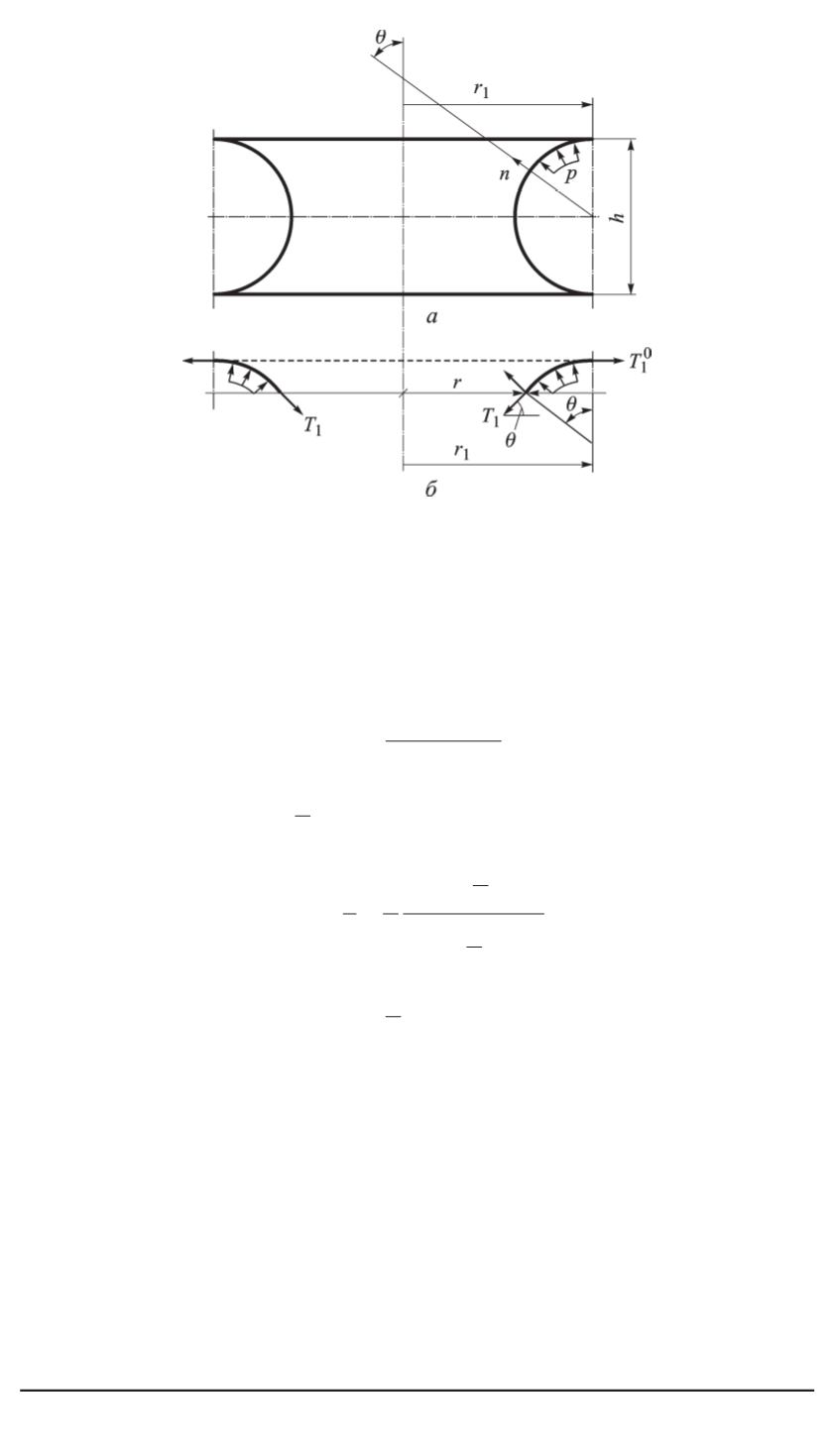
Рис. 3. Расчетная схема торовой оболочки:
a
— схема силового нагружения;
б
— внутренние силовые факторы (
θ
— угол между
нормалью к поверхности оболочки и осью тора)
женных к сегменту торовой оболочки (рис. 3,
б
):
T
1
·
2
πr
sin
θ
=
pπ r
2
1
−
r
2
;
T
1
=
p
(
r
2
1
−
r
2
)
2
r
sin
θ
.
Учитывая, что
r
=
r
1
−
h
2
sin
θ
, представим
Т
1
в виде
T
1
=
1
2
p
h
2
2
r
1
−
h
2
sin
θ
r
1
−
h
2
sin
θ
.
Сила
Т
1
при
θ
= 0
равна
T
1
=
p
h
2
.
Натяжение бислоя
T
1
равно сумме натяжений в двух слоях:
T
1
= 2
Т
1
, а при
θ
= 0
в месте стыка с плоской частью
T
1
= Δ
p
п
h
.
Форма торообразной части остается практически постоянной благо-
даря большой жесткости на растяжение и постоянству величины
Δ
p
п
.
Для определения радиуса поры
r
п
применяются уравнения равновесия
сил, действующих в вырезанном участке оболочки в области поры.
Основной вклад в изменение радиуса поры вносит деформация внеш-
ней области
б
(см. рис. 2). Для того чтобы определить внутренний
радиус поры
r
п
, вычислим радиус отверстия деформированной плос-
кой части мембраны
r
1
и вычтем радиус торообразной части, равный
90
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2012. № 2


