Математическая модель деформирования поры в липидной мембране - page 9

T1 /T1
α = 0 α = 0,
С1 , мкм2 С2 , дин/мкм r1, мкм λ2 , отн.ед r1, мкм λ 2, отн.ед
0,99743 −0 ,3004 ·10−5 0 ,5985 ·10−3 0,99806·10−3 0,499 0,100·10−2 0,51
0,99900 −0 ,2014 ·10−5 0 ,5994 ·10−3 0,14093·10−2 0,705 0,142·10−2 0,71
1,00000 0,2359·10−9 0 ,6000 ·10−3 0,20000·10−2 1 ,00 0,204·10−2 1,02
1,00285 0,948 · 10−3 0 ,6017 ·10−3 0,141·10−1 7 ,05 0 ,16·10−1 8,00
1,00473 0,4915·10−2 0 ,6284 ·10−3 0,713·10−1 35,07 0 ,80·10−1 0,40
1,006655 0,1326 0,6049 ·10−3 0,364 182,07 40 ,00 200 ,00
Вычисление радиуса поры с учетом растяжения площади по-
верхности F = μβ +
1
2
Kα 2 . Соотношения упругости находятся
из выражения для упругого потенциала, в котором учтено изменение
площади:
F = μβ +
1
2
Kα 2 . (16)
Используя (16), получаем
Tr =
μ
2
λ−2
2 − λ−2
1 + K (λ1 λ2 − 1) ,
Tt = −
μ
2
λ−2
2 − λ− 2
1 + K (λ1 λ2 − 1) .
(17)
Разрешающую систему уравнений для определения r и Tr находим из
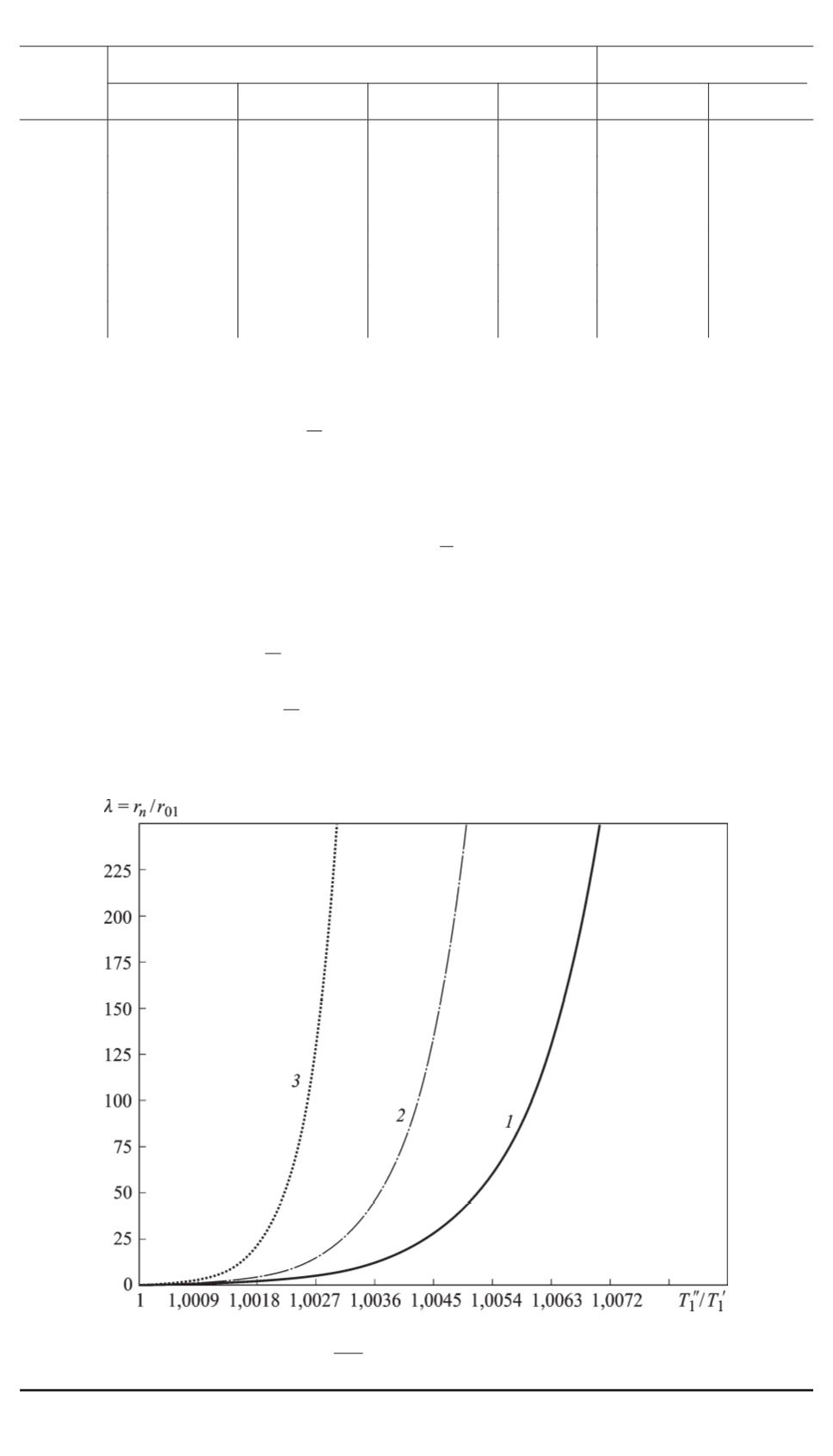
Рис. 6. График зависимости λ
T 1
T 1
при μ=0,003 (1), 0,005 (2), 0,007 дин/см (3)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2012. № 2 95