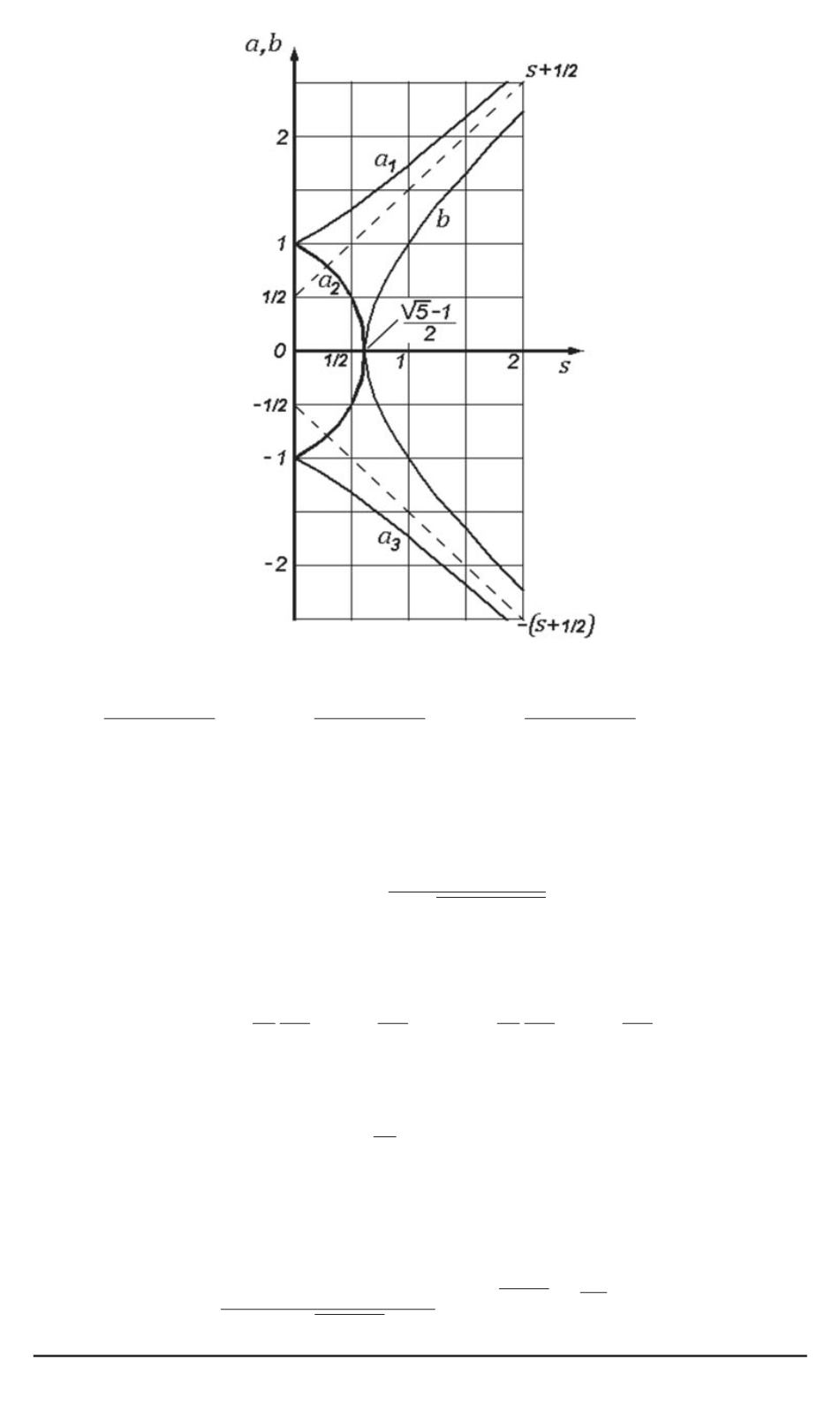
Рис. 2. Графическая интерпретация связи вещественной и мнимой частей
верхнего индекса функции Лежандра со спиновым квантовым числом:
a
1
= 1 +
s
(
s
+ 1)
;
a
2
=
±
1
−
s
(
s
+ 1)
;
a
3
=
−
1 +
s
(
s
+ 1)
9. Поставим в выражение (8) для плотности
ρ
сохраняющейся ве-
личины функцию
Ψ
в виде
Ψ =
Y
(
θ, ϕ
)
f
(
t, r
)
, где в соответствии с
формулой (14)
f
(
t, r
) =
u
μ
n
(
σ
)
r
2
±
(
σ
2
−
1)
.
(19)
Обозначим
ρ
r
=
ρ/
(
Y
¯
Y
)
, тогда из формулы (8) получаем
ρ
r
= ¯
f
r
2
c
∂f
∂t
+
ctr
∂f
∂r
−
f
r
2
c
∂
¯
f
∂t
+
ctr
∂
¯
f
∂r
.
(20)
Используя формулу (19), из (20) после преобразований получаем
ρ
r
=
1
r
3
(
u
¯
u
−
¯
uu
)
.
(21)
И наконец, дифференцируя функцию Лежандра
u
[7], приходим к сле-
дующему:
при
μ
=
a
ρ
r
=
n
(
n
+ 1) +
a
(1
−
a
)
r
3
√
σ
2
−
1
±
u
μ
n
u
μ
−
1
n
−
u
μ
n
u
μ
−
1
n
;
(22)
30
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 3


