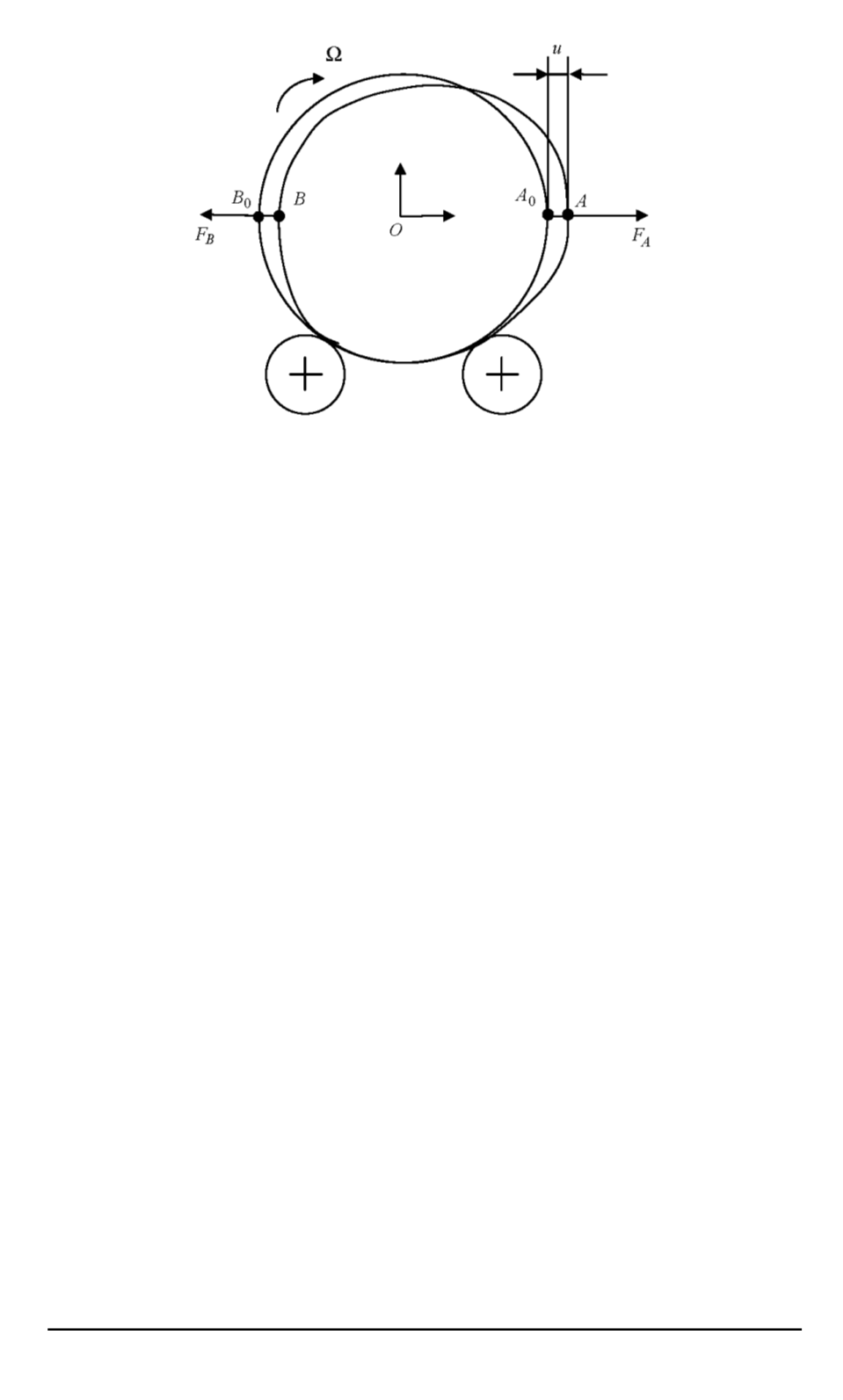
Рис. 2. Силы, возникающие в кольце
Рассмотрим возникновение этого эффекта с точки зрения механи-
ки. Получим зависимости для сил в случае появления колебаний по
первой собственной частоте во вращающемся на двух опорах кольце
радиуса
r
(рис. 2). Для этого найдем зависимости для центробежных
сил, действующих на элементарные массы, находящиеся в точках
A
0
и
В
0
, расположенные симметрично относительно оси вращения (точка
O
). Пусть в результате колебания масса в точке
A
0
из нейтрального
положения сместилась в положение
A
на величину
U
. Тогда ее радиус
относительно оси вращения
O
стал
r
A
=
r
+
U
, а центробежная сила,
действующая на элементарную массу
Δ
m
, равна
F
A
= Δ
m
Ω
2
(
r
+
U
)
.
Для точки
B
0
радиус уменьшится примерно на величину
U
и станет
r
B
=
r
−
U
, а центробежная сила, действующая на такую же элементар-
ную массу, равна
F
B
= Δ
m
Ω
2
(
r
−
U
)
. Суммарная результирующая цен-
тробежная сила от этих элементарных масс
F
=
F
A
−
F
B
= 2Δ
m
Ω
2
U
.
Суммарная сила, действующая на кольцо и возвращающая его в
нейтральное положение, которая учитывает силу упругости и центро-
бежные силы от элементарных масс в точках
A
и
B
, выражается как
F
Δ
m
=
F
y
−
F
=
F
y
(
U
)
−
2Δ
m
Ω
2
U.
Здесь
F
y
— сила упругости кольца, возвращающая его в нейтральное
положение, зависит от отклонения
U
.
Из последней формулы видно, что результирующая сила, от ко-
торой зависит частота собственных колебаний, определяется угловой
скоростью вращения кольца
Ω
, с увеличением которой она уменьша-
ется. Вычисляя интеграл для этой силы по всему кольцу, получаем,
что с увеличением угловой скорости вращения кольца сила, возвра-
щающая кольцо в нейтральное положение, уменьшается, а значит, и
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 1
47


