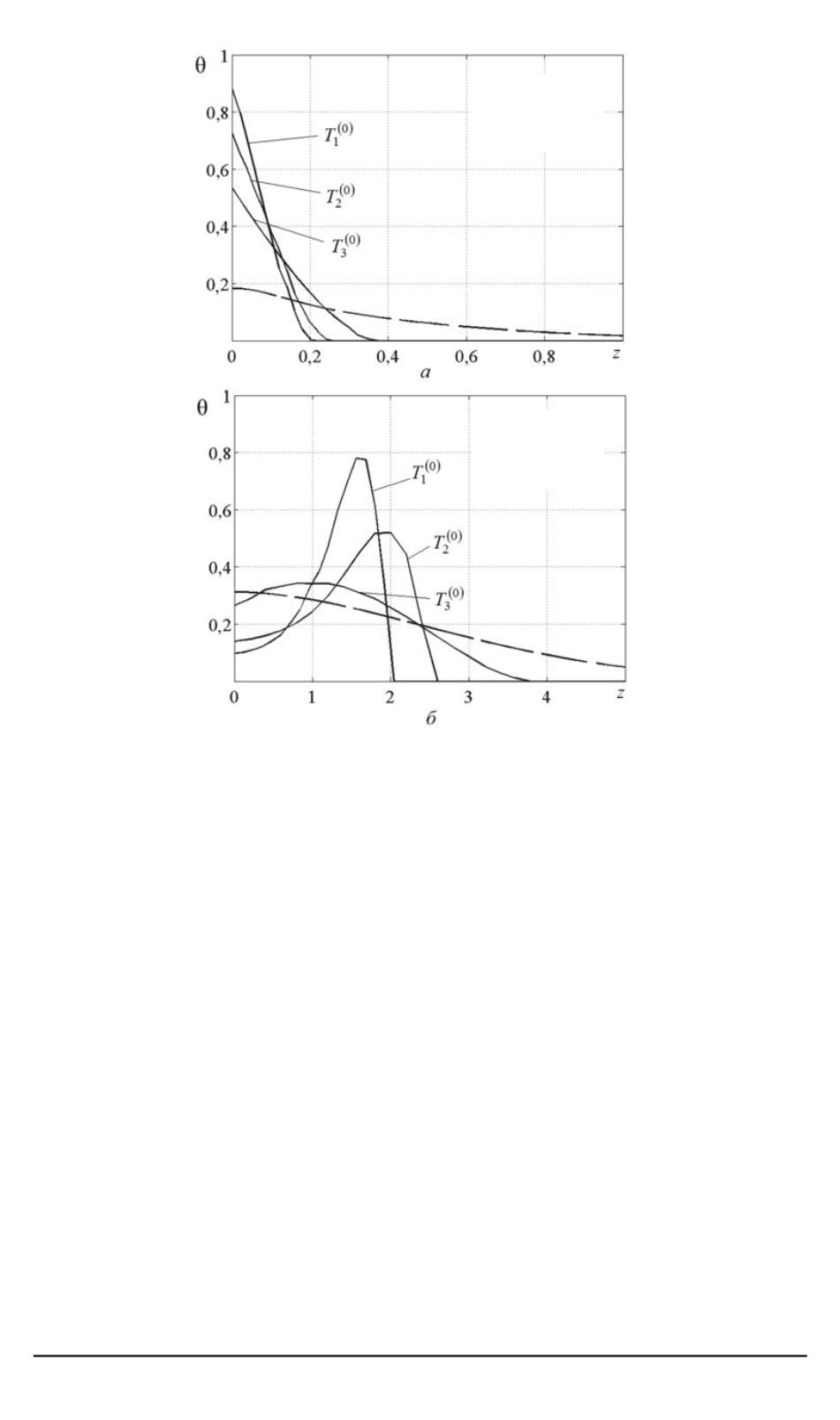
Рис. 3. Распределение температуры по глубине полупространства
z
при
D
2
q
= 10
,
D
2
T
= 10
(сплошные кривые — расчет по формуле (24), штриховые
кривые — параболическое уравнение теплопроводности):
a
—
¯
t
= 0
,
5
;
б
—
¯
t
= 5
Из приведенных рисунков можно сделатьвывод, что различия в
температурных полях тем больше, чем больше значение параметра
D
2
q
, т.е. чем меньше скорость распространения теплоты.
Также очевидно, что температура при
T
(0)
=
T
(0)
1
значительно
выше, чем при
T
(0)
=
T
(0)
2
и
T
(0)
=
T
(0)
3
. Это можно объяснить
тем, что в матрице
T
(0)
1
все недиагональные элементы равны нулю,
что, в свою очередь, говорит о меньшем рассеянии энергии. А при
T
(0)
=
T
(0)
3
теплота быстрее проникает вглубьсреды, что обусловлено
тем, что элемент
T
(0)
3
11
больше остальных диагональных элементов,
и
T
(0)
3
23
=
T
(0)
3
32
= 0
. Таким образом, расположение нанострук-
турных элементов в объеме влияет на распределение температуры.
Выводы.
На основе соотношений рациональной термодинами-
ки предложена математическая модельпроцесса теплопроводности в
84
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 3


