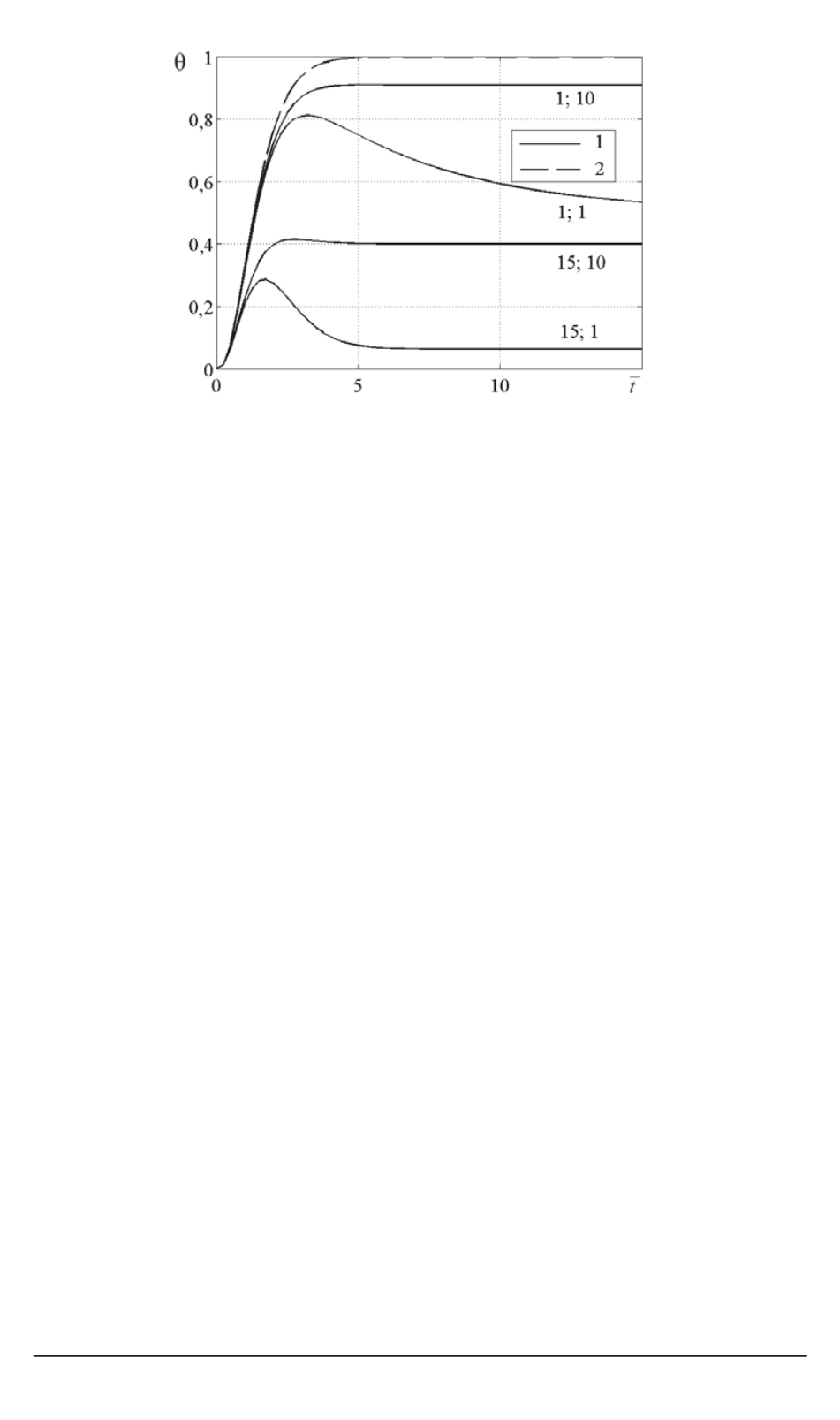
Рис. 1. Зависимость средней по объему температуры
θ
от времени
¯
t
:
сплошные кривые — расчет по формуле (17); штриховая кривая — параболическая
теплопроводность; цифры у кривых — соответственно значения
˜
c
и
A
44
из (8) получим
χ
j
=
B
ji
¯
χ
i
,
B
ji
=
A
−
1
ij
и в соответствии с (12) имеем
q
i
=
ϕ
ik
B
kj
¯
χ
j
=
−
ϕ
ik
B
km
Z
(1)
mj
∂T/∂x
j
=
−
Λ
ij
∂T/∂x
j
,
где
Λ
ij
=
ϕ
ik
B
km
Z
(1)
mj
— компоненты тензора теплопроводности нано-
структурных материалов. Следует отметить, что параметры
B
ij
=
B
ji
позволяют учестьлокальную анизотропию теплопроводности нано-
структурных материалов при изотропии материалов в макромасштабе.
Для массивных материалов
B
km
=
δ
km
и компоненты тензора тепло-
проводности
λ
ij
=
ϕ
ik
δ
km
Z
(1)
mj
=
ϕ
ik
Z
(1)
kj
и
ϕ
ik
=
ϕ
ki
,
Z
(1)
kj
=
Z
(1)
jk
[3–6].
Так как теплопроводностьнаноструктурных материалов складывает-
ся из электронной и решеточной составляющих (для металлов пре-
обладает первая, для полупроводников и диэлектриков — вторая), то
снижение теплопроводности нанометаллов обусловлено рассеянием
электронов на межзеренных границах, а для диэлектриков и полупро-
водников — рассеянием фононов на поверхностях раздела элементов
наноструктуры [1]. Введение в определяющие уравнения параметров
B
ij
позволяет учестьэти процессы при построении феноменологиче-
ской модели.
Действительно, для изотропных массивных материалов возможны
только два варианта получения выражения для
λ
. В первом вариан-
те
ϕ
ik
=
ϕ
0
δ
ik
и
Z
(1)
kj
=
Z
0
δ
kj
, тогда
λ
ij
=
ϕ
0
Z
0
δ
ik
δ
kj
=
λδ
ij
. Во
втором варианте
ϕ
ik
=
ϕ
0
ϕ
(0)
ik
,
Z
(1)
kj
=
Z
0
Z
(0)
kj
и
Z
(0)
kj
= (
ϕ
(0)
jk
)
−
1
(или
ϕ
(0)
ik
= (
Z
(0)
ki
)
−
1
)
, тогда
λ
ij
=
ϕ
0
Z
0
ϕ
(0)
ik
Z
(0)
kj
=
ϕ
0
Z
0
δ
ij
=
λδ
ij
. Следо-
вательно, для анизотропных на микроуровне массивных материалов
во втором варианте также возможна изотропия теплопроводности на
78
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 3


