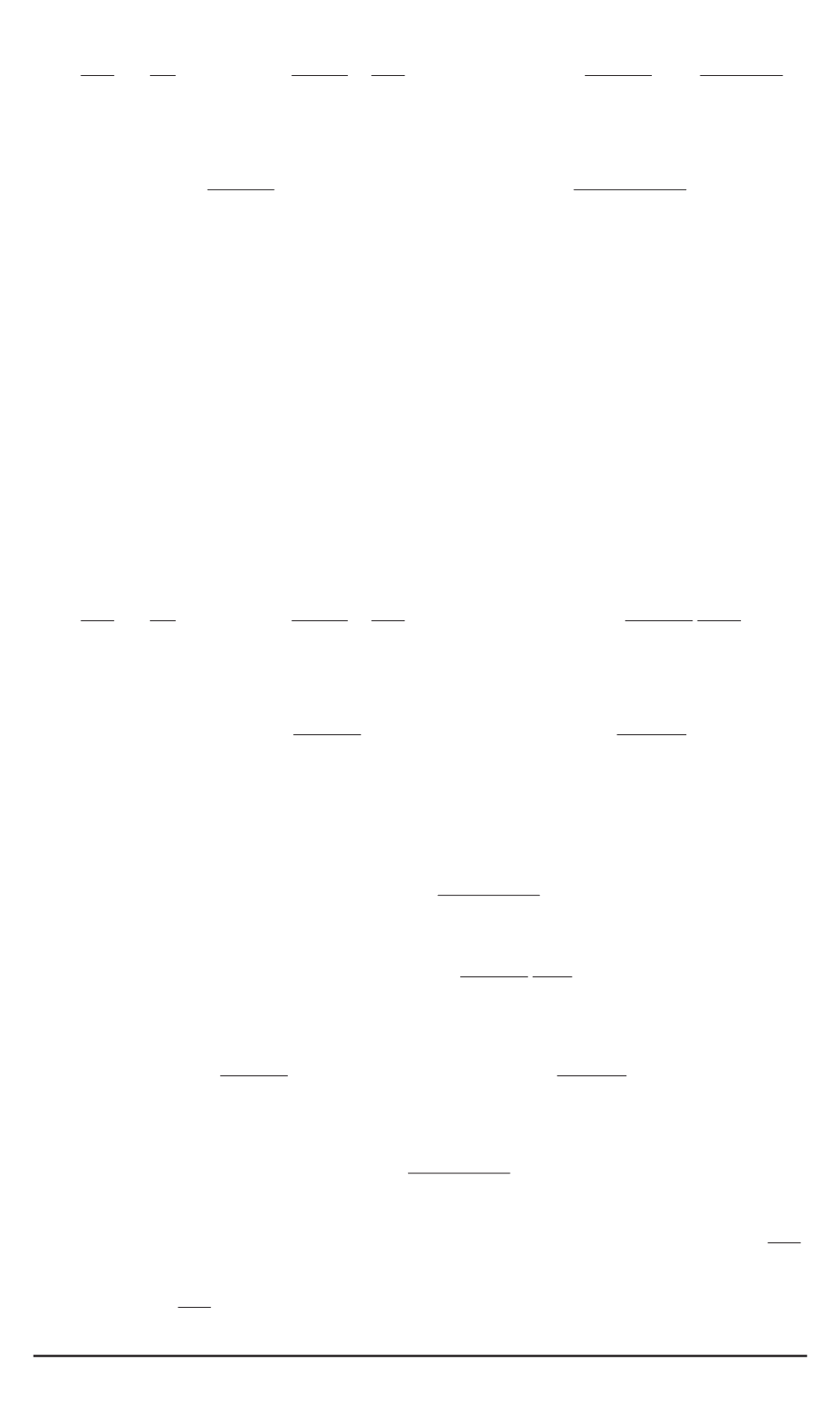
ρc
∂T
∂t
+
ρc
τ
T
t
0
exp
−
t
−
t
τ
T
∂T
∂t
dt
=
μ
=1
,
2
,
3
ϕ
ij
α
jμ
C
μ
λ
μ
Z
1
m
∂
2
T
∂x
i
∂x
m
−
−
ϕ
ij
α
jμ
C
μ
λ
μ
Z
1
m
t
0
exp
−
λ
μ
(
t
−
t
)
/τ
q
∂
3
T
∂t ∂x
i
∂x
m
dt ,
(19)
где
λ
μ
— собственные значения однородной системы, соответствую-
щей (18);
(
α
1
μ
α
2
μ
α
3
μ
)
т
— собственные векторы;
C
μ
— некоторые кон-
станты, полностью определяемые компонентами
τ
(
q
)
ij
.
Расчет температурных полей в полном объеме представляет собой
сложную задачу. Оценим влияние параметров нагрева на распределе-
ние температуры, используя одномерную расчетную схему, предпола-
гая, что температура зависит только от координаты
x
1
, направленной
вглубьполупространства, и времени
t
.
В одномерном случае уравнение теплопроводности будет иметь
вид
ρc
∂T
∂t
+
ρc
τ
T
t
0
exp
−
t
−
t
τ
T
∂T
∂t
dt
=
μ
=1
,
2
,
3
ϕ
11
Z
11
α
1
μ
C
μ
λ
μ
∂
2
T
∂x
2
1
−
−
ϕ
11
Z
11
α
1
μ
C
μ
λ
μ
t
0
exp
−
λ
μ
(
t
−
t
)
/τ
q
∂
3
T
∂t ∂x
2
1
dt .
(20)
Начальные и краевые условия для такой модели поверхностного
нагрева запишем в виде
T
(
x
1
, t
)
|
t
=0
=
T
0
,
∂T
(
x
1
, t
)
∂t
t
=0
= 0;
x
= 0 :
−
ϕ
11
Z
11
α
1
μ
C
μ
λ
μ
∂T
∂x
1
+
+
ϕ
11
Z
11
α
1
μ
C
μ
λ
μ
t
0
exp (
−
λ
μ
(
t
−
t
)
/τ
q
)
∂
2
T
∂t ∂x
1
dt
=
q
s
;
x
→ ∞
:
∂T
(
x
1
, t
)
∂x
= 0
,
(21)
где
q
s
=
BMt
m
exp (
−
mt/t
0
)
,
m
1
,
m
∈
N
.
Если ввести безразмерные параметры и переменные
z
=
x
1
/
√
at
0
,
¯
t
=
t/t
0
;
θ
= (
T
−
T
0
)
/T
∗
;
D
2
q
=
τ
q
/t
0
;
D
2
T
=
τ
T
/t
0
;
˜
C
i
=
α
1
i
C
i
/λ
i
;
T
∗
=
Bt
m
0
√
at
0
/λ
(
T
)
;
a
=
λ
(
t
)
/
(
ρc
)
;
q
0
( ¯
t
) =
M
¯
t
m
exp(
−
m
¯
t
)
;
M
=
80
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 3