суммирование, можно оценить точность приближения. Однако в рас-
сматриваемой задаче подобное упорядочение слагаемых по величине
не имеет места, поэтому нельзя воспользоваться “обычной” теорией
возмущений.
Обратим внимание на то, что в
M
(334)
3
,
M
(3344)
4
и прочих выраже-
ниях высших порядков по взаимодействию присутствуют сразу трех-
и четырехфононные вершины. Данный факт дает возможность учесть
взаимное влияние этих процессов релаксации и проверить для кон-
кретных типов кристаллов степень справедливости предположения о
независимости процессов рассеяния. Результатом такого допущения
является широко распространенное соотношение
Γ =
i
Γ
i
, смысл
которого заключается в том, что полная скорость релаксации фоно-
нов
Γ
может быть представлена в виде суммы скоростей релаксации
в результате
i
-х механизмов рассеяния
Γ
i
.
Используя набор стандартных правил (изложенных, например, в
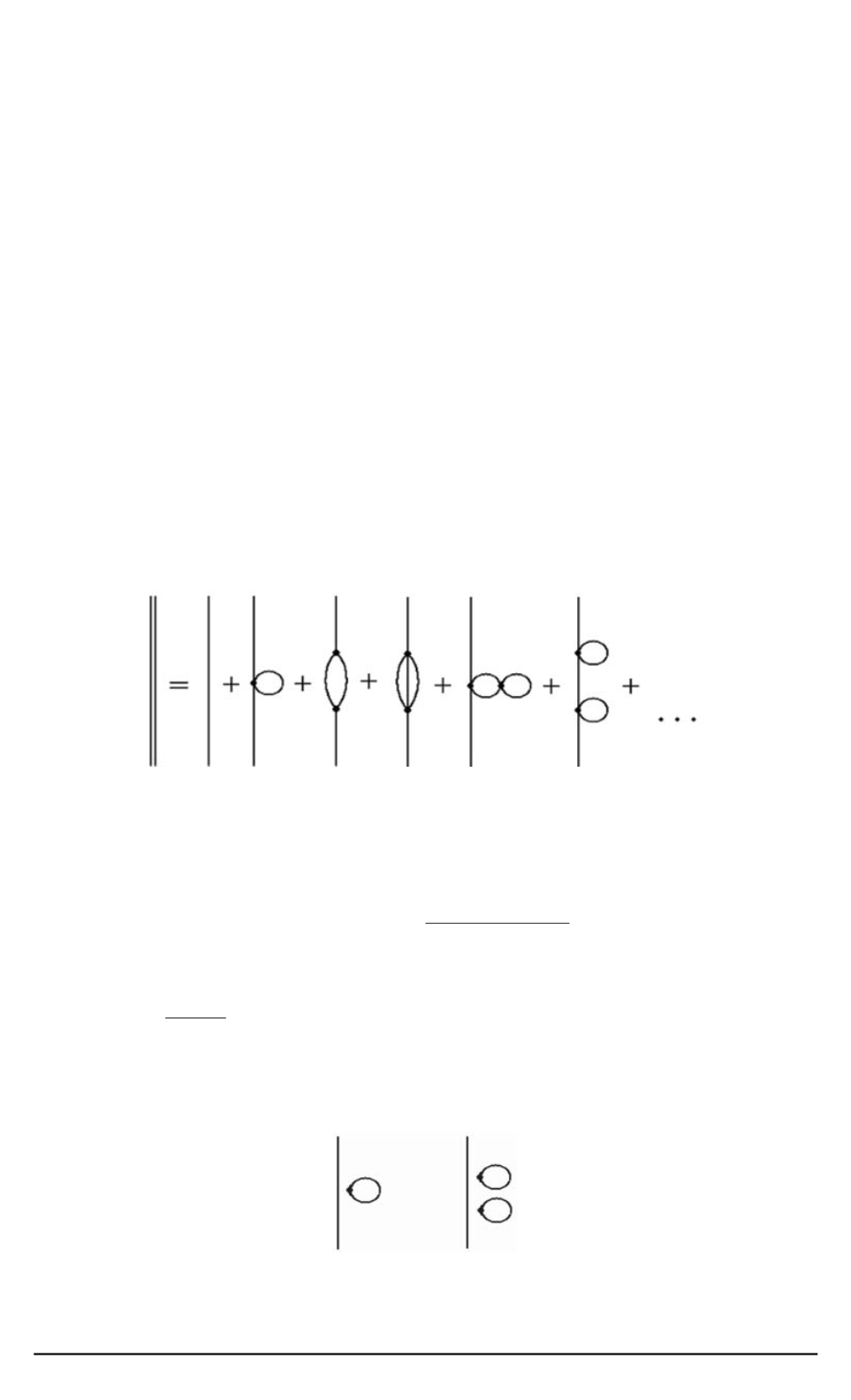
[8–10]), полезно представить виковское разложение функции Грина
(5) с помощью фейнмановских диаграмм:
(6)
Здесь — фурье-трансформанта одночастичной мацубаровской функ-
ции Грина фонона;
|
— фурье-трансформанта мацубаровской функции
Грина свободного фонона [9]
D
(0)
kj
(
ω
s
) =
−
2
k
B
Tω
kj
ω
2
kj
+
ω
2
s
,
где
ω
s
=
πs
2
k
B
T
— дискретная частота;
s
— целое число.
Из теоремы о разложении функции Грина по связанным группам
[10] следует, что при написании ряда (6) несвязанные диаграммы,
например
учитывать не следует, так как они необходимы лишь для избавления
от знаменателя в виковском разложении функции Грина (5).
54
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 4


