Восстановление закономерности изменения вида деформированного состояния и сдвиговых характеристик пластических материалов - page 7

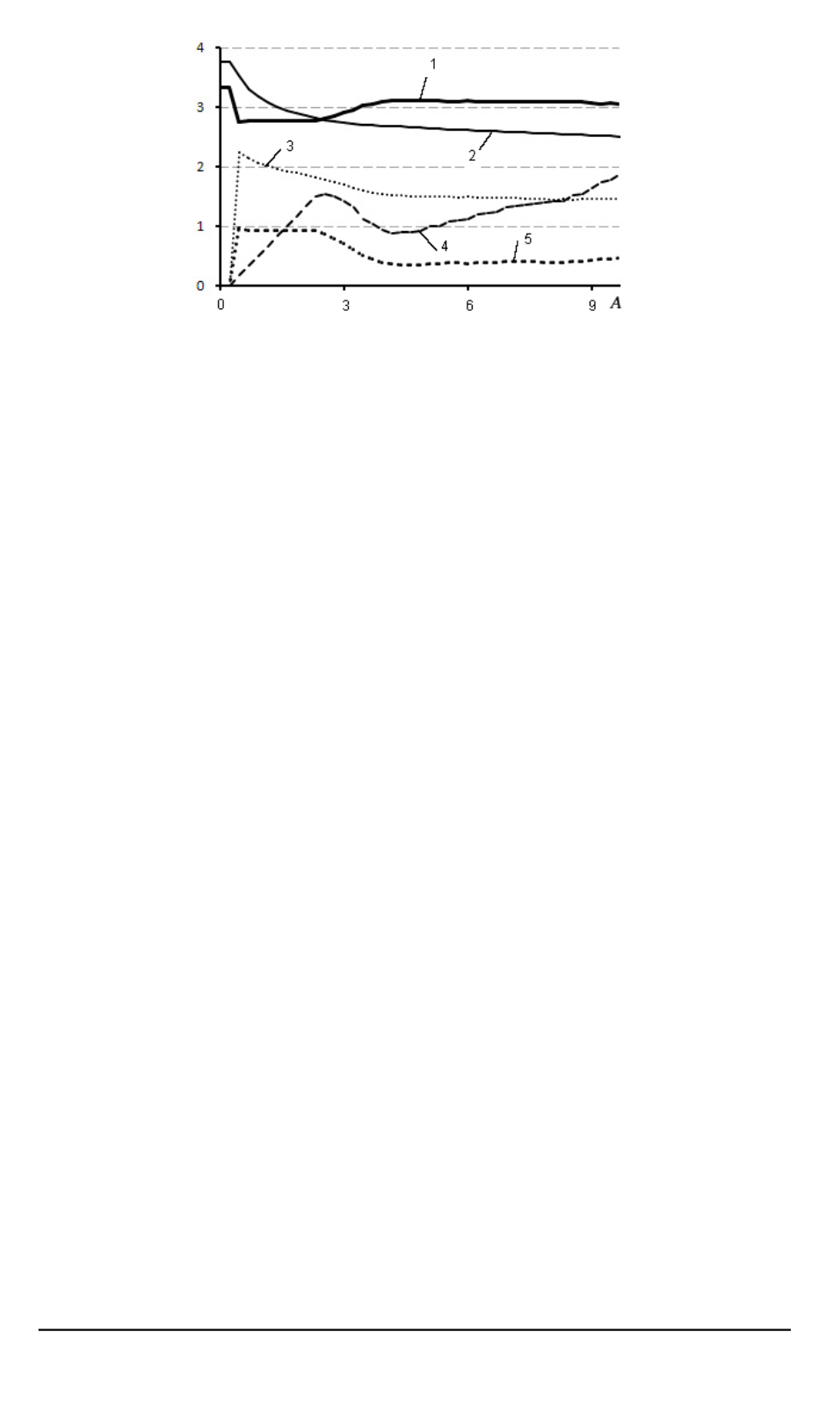
Рис. 2. Зависимость механических характеристик от А :
1 — υ × 6; 2 — ln Gυ /3; 3 — ln Gd /4; 4 — Фd × (5 ∙ 104); 5 — tg ω × 10
об изменении интенсивности деформаций. Поскольку кривые для со-
ответствующих характеристик жесткости почти накладываются друг
на друга, убывающая кривая 5 представлена для ln Gp .
Ниже в графическом виде приведены результаты численного ис-
следования. На рис. 2 все графики относятся к θ = θ0, при котором
отклонение от подобия достигает максимального значения. Кривая 1
представляет искомую закономерность изменения угла вида деформи-
рованного состояния в зависимости от A. Кривые 2 и 3 дают предста-
вление об изменении характеристик жесткости графиками для ln Gυ и
ln Gd .
Поведение характеристик Фd и tg ω иллюстрируется кривыми 4 и 5.
Пока материал деформируется линейно и упруго, величины Gd , Фd и
tg ω равны нулю, а Gυ и υ имеют постоянные значения. При появлении
пластической деформации возрастает значение Ф d, а кривые для Gd и
tg ω имеют всплеск практически на всей площадке текучести. На этом
же участке наблюдается резкое снижение угла υ , значения которого
затем постепенно восстанавливаются, оставаясь ниже угла θ.
Более наглядно рассматриваемая закономерность представлена на
рис. 3, где графики иллюстрируют изменения угла υ в зависимости от
А. Угол θ от одной кривой к другой изменяется на пять градусов. Кри-
вая 1 соответствует растяжению, кривая 2 — чистому сдвигу, кривая
3 — простому сжатию. Первый и последний графики — прямые линии,
поскольку при растяжении и сжатии ω = 0, υ = θ.
Отмеченные циклы вычислений можно провести также при A =
= const c шагом по оси θ в 2−3 градуса. На рис. 4 иллюстрируется
зависимость сдвиговых характеристик от вида напряженного состоя-
ния. Кривая 1 относится к податливости Фθ , кривая 2 — к Фm. Кривая
3 представляет зависимость υ = f (θ) , кривая 4 относится к характе-
ристике G d, ее зеркальное отражение — кривая 5, представляющая Фd .
Кривая 6 показывает изменение tg ω. Значение tg ωmax соответствует
θ0 = 31,8◦ .
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 2 87