венств. Вид соответствующих неравенств зависит от значений трех
параметров системы. Рассмотрим частный случай
β
= 3
,
σ
= 10
,
ρ
= 30
. В этом случае выполняются неравенства
β <
2
σ
,
σ >
2
,
σ >
2
β
. Следовательно, локализирующее множество описывается
системой неравенств
y
2
1
+
y
2
2
+ (
z
−
ρ
)
2
≤
K
βσ
ρ
2
;
x
2
1
+
x
2
2
≤
2
σz
+2
C
βσ
σρ
+2
σ
q
C
βσ
K
βσ
ρ
2
−
y
2
1
−
y
2
2
−
(
z
−
ρ
)
2
;
x
2
1
+
x
2
2
≤
2
σz
;
y
2
1
+
y
2
2
+ (
z
−
ρ
)
2
≤
K
β
1
ρ
2
;
x
2
1
+
x
2
2
≤
σ
σ
−
2
y
2
1
+
y
2
2
+ (
z
−
ρ
)
2
+
β
2
ρ
2
(
σ
−
2)(
σ
−
2
β
)
.
(12)
Так как в данном случае
K
βσ
=
K
β
1
, первое и четвертое нера-
венства системы (12) совпадают. Третье неравенство включает второе,
поскольку
C
βσ
>
0
. Таким образом, число неравенств в системе (12)
можно уменьшить:
(
y
2
1
+
y
2
2
+ (
z
−
ρ
)
2
≤
K
βσ
ρ
2
;
x
2
1
+
x
2
2
≤
f
(
y
1
, y
2
, z
)
,
(13)
где
f
(
y
1
, y
2
, z
) = min 2
σz
;
σ
σ
−
2
y
2
1
+
y
2
2
+ (
z
−
ρ
)
2
+
β
2
ρ
2
(
σ
−
2)(
σ
−
2
β
)
.
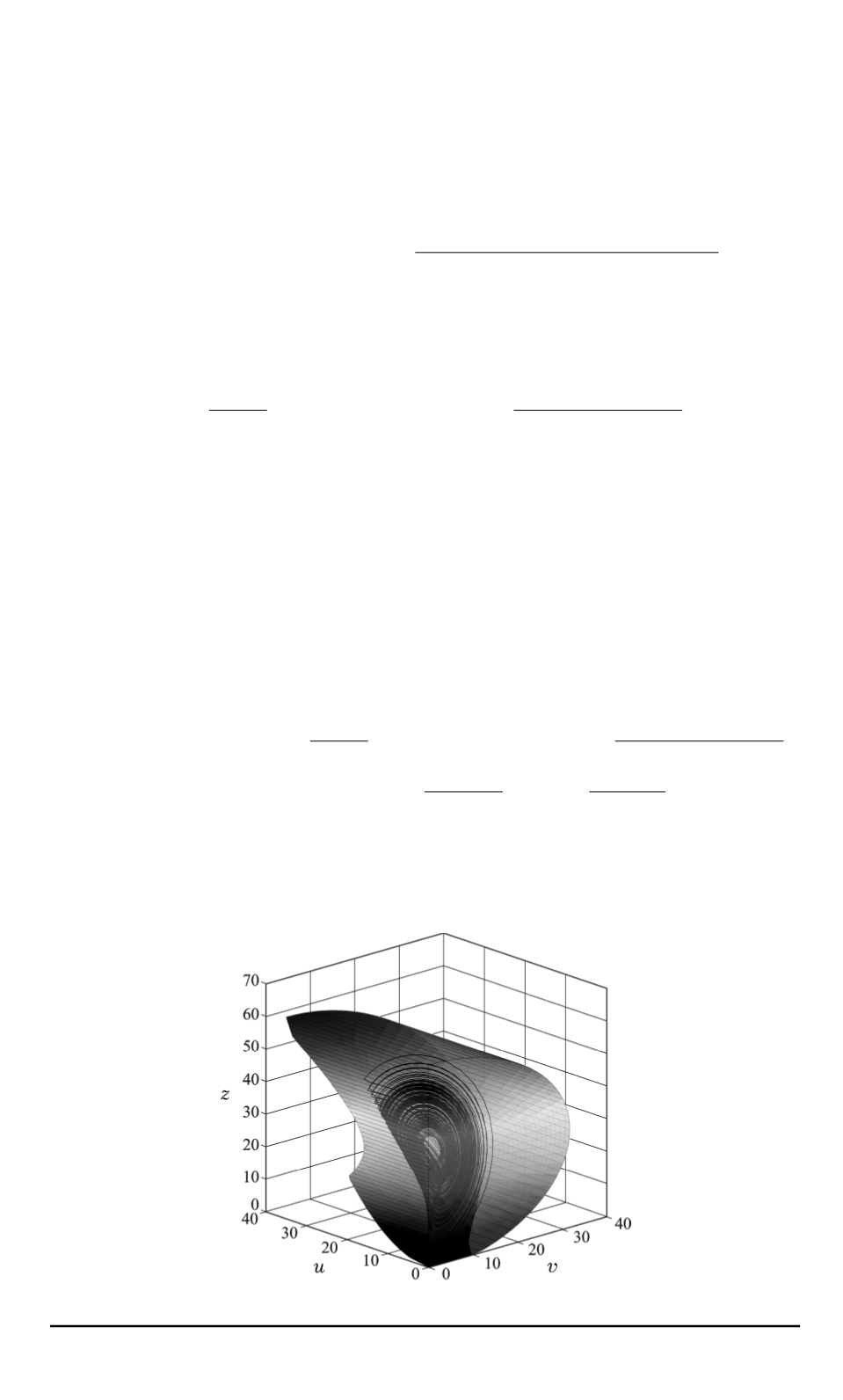
На рис. 2 в переменных
u
=
p
x
2
1
+
x
2
2
,
v
=
p
y
2
1
+
y
2
2
,
z
показаны
траектория системы с начальными условиями
x
1
= 1
,
x
2
=
x
3
=
y
1
=
=
y
2
=
z
= 0
и локализирующее множество (13).
Рис. 2. Траектория системы и локализующее множество
14
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 4


