(1 +
λσ
)
U
= 0;
(1 +
λ
)
V
= 0;
(1 +
λβ
)
Z
+
λβd
= 0;
σU
2
+
V
2
+
β
(
Z
+
d
)
2
=
βd
2
.
Очевидные решения системы
U
=
V
=
Z
= 0
,
λ
= 0
и
U
=
V
= 0
,
Z
=
−
2
d
,
λ
=
−
2
/β
дают глобальный минимум
F
1
= 0
целевой функ-
ции и значение
F
2
= 4
d
2
. Вариант
λ
=
−
1
(из второго уравнения)
возможен при
β
≥
2
и дает третье значение
F
3
=
β
2
d
2
β
−
1
целевой функ-
ции в точках
U
= 0
,
V
=
±
βd
β
−
1
√
β
−
2
,
Z
=
−
βd
β
−
1
. Отметим,
что при
β
≥
2
выполняется неравенство
β
2
d
2
β
−
1
≥
4
d
2
. Наконец, ва-
риант
λ
=
−
1
/σ
реализуется при
β
≥
2
σ
и дает четвертое значение
F
4
=
β
2
d
2
σ
(
β
−
σ
)
, причем
F
4
≥
4
d
2
при
β
≥
2
σ
.
Итак, максимум функции
ϕ
на универсальном сечении есть одно
из значений
F
2
= 4
d
2
,
F
3
=
β
2
d
2
β
−
1
,
F
4
=
β
2
d
2
σ
(
β
−
σ
)
в зависимости от
взаимного расположения трех значений:
1
,
σ
и
β/
2
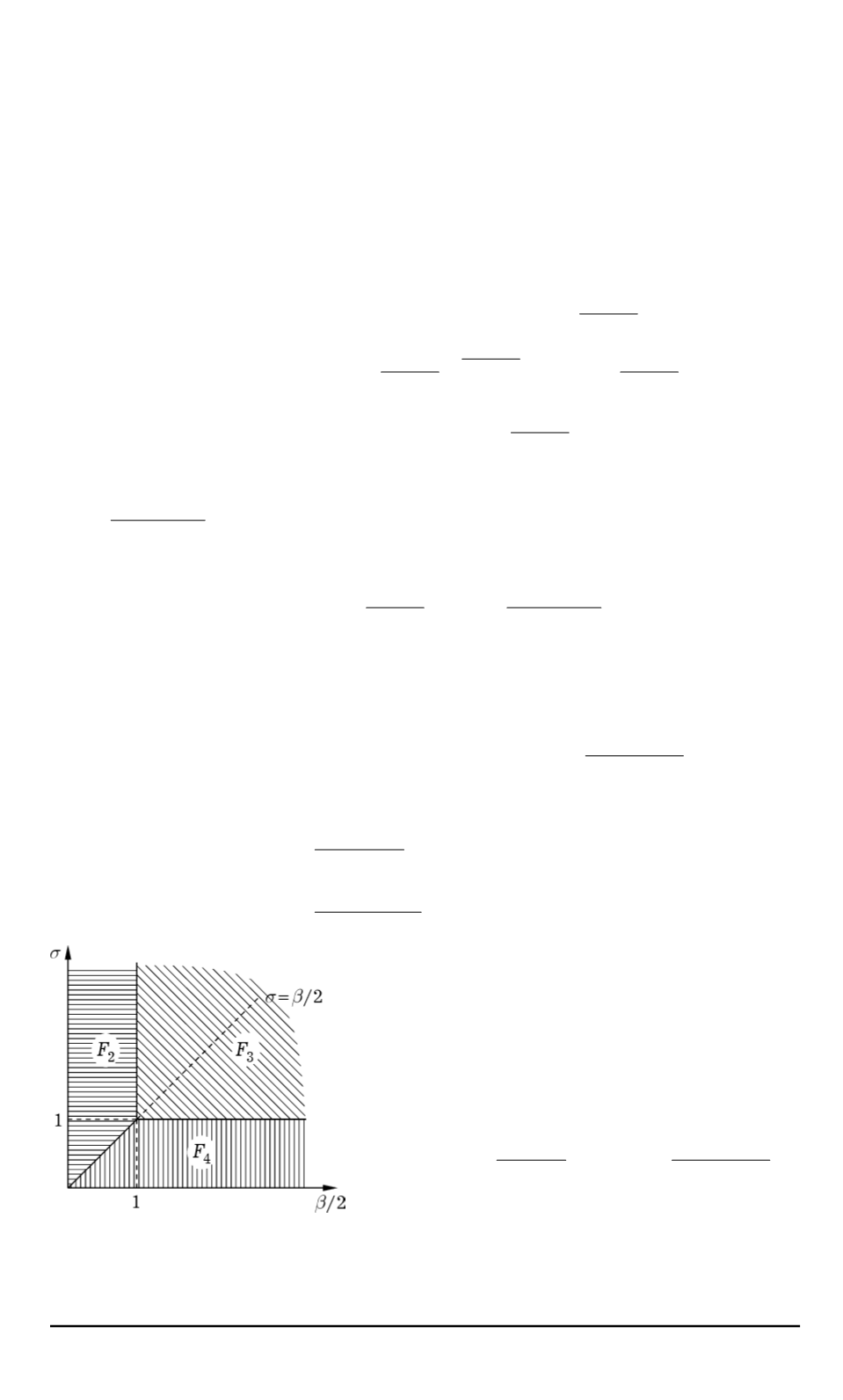
. На рис. 1 показана
область изменения параметров
β
,
σ
, разделенная на три подобласти в
соответствии с тем, какое из трех значений дает максимум функции
ϕ
.
Исходя из рис. 1, можно записать, что
ϕ
sup
=
K
βσ
(
σ
+
qρ
)
2
q
, где
K
βσ
=
1
,
β
≤
2
σ, β
≤
2;
β
2
4(
β
−
1)
,
β >
2
,
σ >
1;
β
2
4
σ
(
β
−
σ
)
, β >
2
σ, σ
≤
1
.
(6)
Рис. 1. Область изменения па-
раметров системы, обеспечива-
ющих максимум целевой функ-
ции
ϕ
Мы имеем однопараметрическое
семейство локализирующих множеств
Ω
1
(
q
) = Ω(0
,
0
, q
)
,
q >
0
, описываемое
неравенством
x
2
1
+
x
2
2
+
qy
2
1
+
qy
2
2
+
+
q z
−
σ
+
qρ
q
2
≤
K
βσ
(
σ
+
qρ
)
2
q
.
Найдем пересечение этого семейства.
Умножим неравенство на
q
и запи-
шем в виде
Aq
2
+
Bq
+
C
≥
0
:
10
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 4


