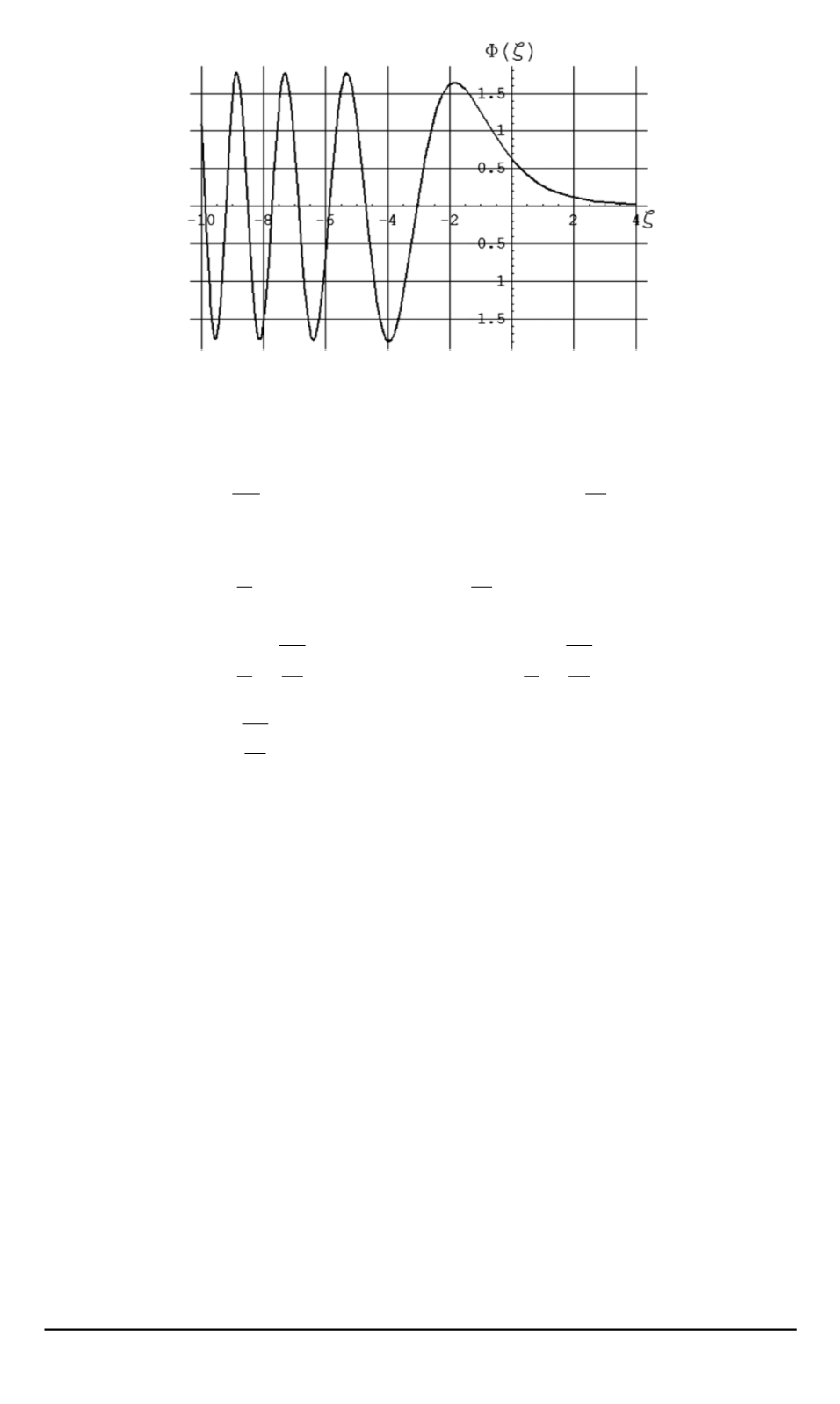
Рис. 3. Вид функции
Φ(
ζ
)
вместо (15) получим
G
(
x, x
0
, t
) =
1
2
π
∞
Z
−∞
exp
i k
(
x
−
x
0
)
−
c
0
k
+
δ
c
0
k
|
k
|
t dk
=
=
1
π
∞
Z
0
cos
k
(
x
−
x
0
) +
δ
c
0
k
2
t dk
=
=
1
π
r
δt
c
0
∞
R
0
cos [
ζu
+
u
2
]
du
=
1
π
r
δt
c
0
Φ (
ζ
)
,
где
ζ
= (
x
−
x
0
)
r
c
0
δt
.
Из графика функции
Φ(
ζ
)
(рис. 3) видно, что при положительных
значениях аргумента
Φ(
ζ
)
стремится к нулю, при отрицательных имеет
бесконечный незатухающий осциллирующий “хвост”.
Заключение.
В работе выявлены основные свойства законов дис-
персии для поверхностных волн и на основе самых общих соображе-
ний показано, что частота является четной функцией волнового числа,
а коэффициент затухания — нечетной. Для полученного дисперсионно-
го уравнения выделено несколько характерных случаев, соответствую-
щих различным режимам. Полученные выражения положены в основу
анализа временной эволюции волновых пакетов. Получена функция
Грина задачи об эволюции профиля волн, распространяющихся на по-
верхности тяжелой заряженной жидкости с учетом поверхностного
натяжения.
СПИСОК ЛИТЕРАТУРЫ
1. А н т о н ю к П. Н. Дисперсионное уравнение для плоской капиллярно-
гравитационной волны на свободной поверхности вязкой несжимаемой жид-
кости // ДАН СССР. – 1986. – Т. 286. – № 6. – С. 1324–1328.
68
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 1


