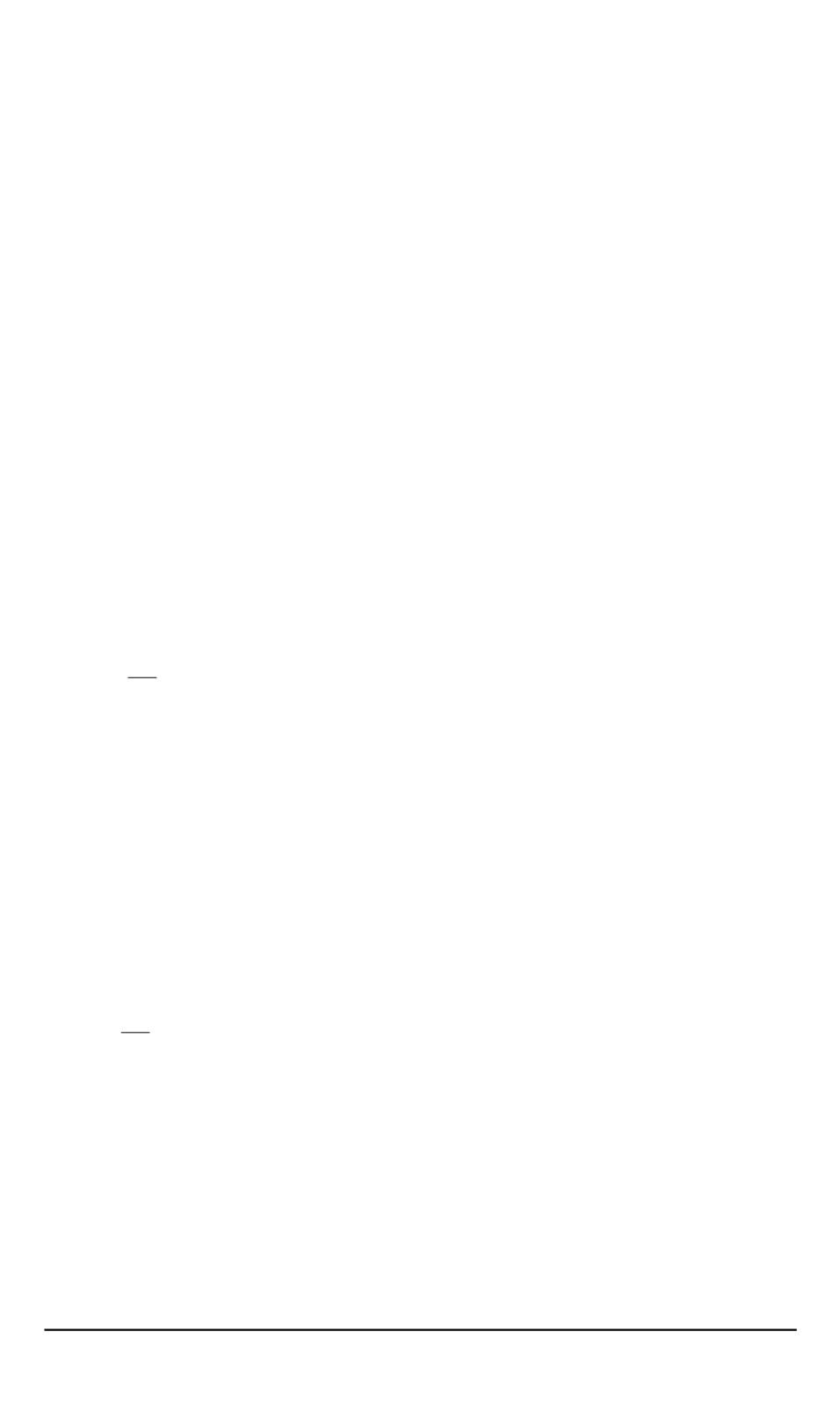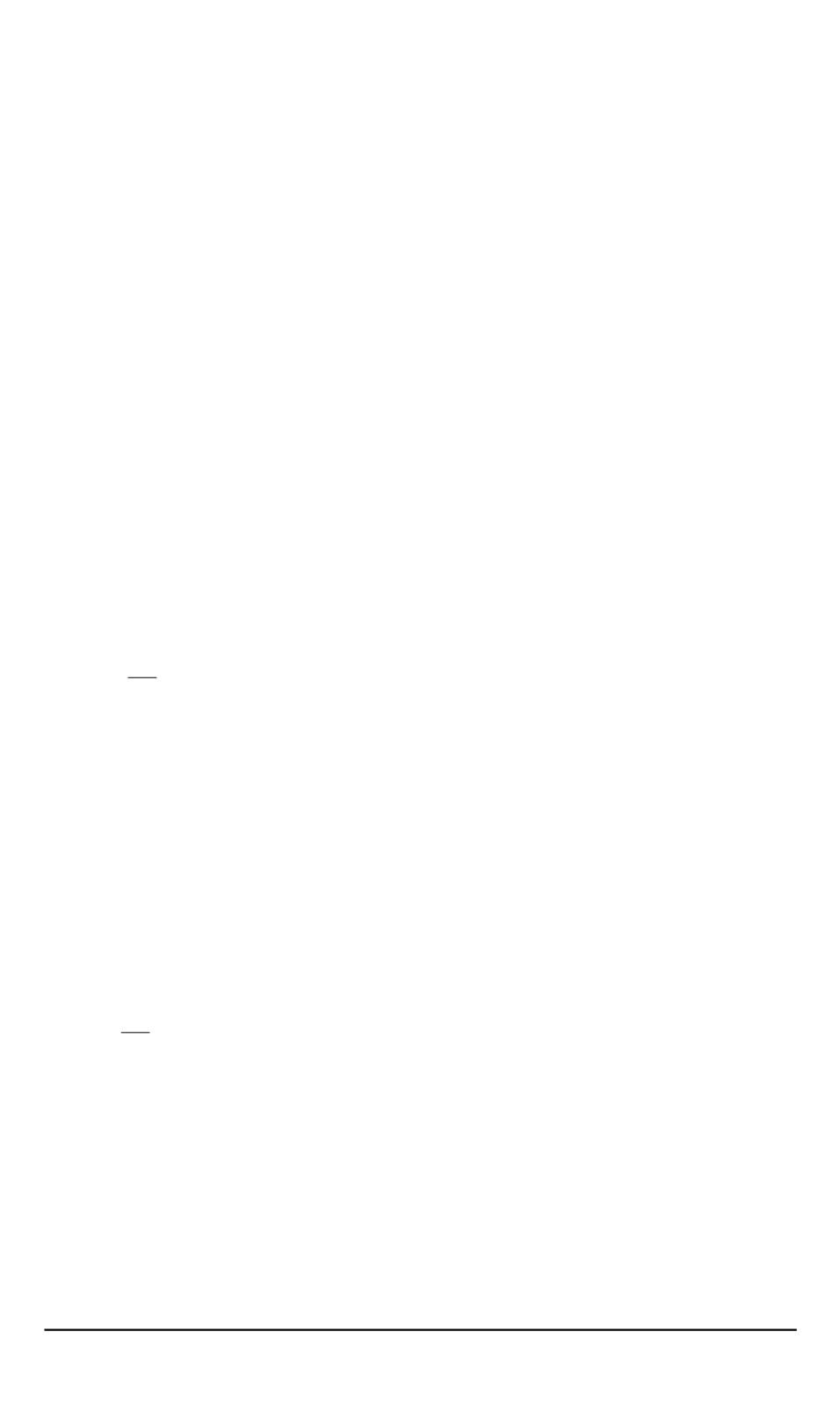
а с учетом (15) будем иметь
E
(
I
n
−
j
ε
n
−
j
ε
n
−
r
−
j
) =
s
n
−
j
s
n
−
r
−
j
(
E
ε
−
1
)
2
2
1
−
r
E
(
I
n
−
r
−
j
−
1
) +
o
(1)
.
Подставляя это равенство в (17) и учитывая (см. (13)), что
E
I
n
= 2
−
n
+
+
o
(1)
, получаем, что для
j >
2
E
(
I
n
−
1
−
r
ε
n
−
j
ε
n
−
r
−
j
) =
s
n
−
j
s
n
−
r
−
j
(
E
ε
−
1
)
2
2
3
−
n
+
r
+
o
(1)
.
Подставив это выражение и (15) в формулу (16), получим, что для
j >
2
E
(
I
n
−
1
ε
n
−
j
) =
−
2
1
−
j
(
E
ε
−
1
)
E
(
I
n
−
j
−
1
)
s
n
−
j
+
+
s
n
−
j
G
0
(0)(
E
ε
−
1
)
2
2
4
−
n
α
j
j
−
1
X
r
=1
s
n
−
r
s
n
−
j
−
r
+
q
X
k
=1
k
6
=
j
c
k
α
k
+
o
(
|
α
|
)
,
где
c
k
,
k
= 1
, . . . , q
,
k
6
=
j
— некоторые постоянные.
Таким образом, отсюда и из (15) найдем, что при
n >
2
q
P
n
(
s, α
) = 2
−
1
P
n
−
1
(
s, α
) +
A
q
X
j
=1
α
j
s
n
s
n
−
j
2
−
j
−
1
P
n
−
j
−
1
(
s, α
)+
+
A
2
2
n
q
X
j
=2
α
2
j
j
−
1
X
r
=1
s
n
s
n
−
j
s
n
−
r
s
n
−
j
−
r
+
q
X
k,j
=1
k
6
=
j
c
kj
α
k
α
j
+
o
|
α
|
2
,
(18)
где
A
=
−
4
G
0
(0)
E
ε
−
1
.
Легко видеть, что эта формула остается справедливой и для
n
≤
2
q
,
если положить по определению
P
0
(
s, α
) = 1
и
P
k
(
s, α
) = 0
для всех
k <
0
. Применяя эту формулу рекуррентным образом
n
−
1
раз, будем
иметь
P
n
(
s, α
) = 2
−
n
(
1 +
A
q
X
j
=1
α
j
n
X
k
=
j
+1
s
k
s
k
−
j
+
+
A
2
2
q
X
j
=1
α
2
j
n
X
k
=
j
+1
s
k
s
k
−
j
!
2
−
(
n
−
j
)
−
2
n
X
k
=2
j
+1
s
k
s
k
−
2
j
+
+
q
X
j,r
=1
r
6
=
j
c
rj
α
r
α
j
+
o
|
α
|
2
,
откуда с учетом (4) получим (9). Лемма доказана.
Доказательство леммы 1.
Как видно из вывода (18), при дока-
зательстве этого соотношения с точностью до
o
(
|
α
|
)
функцию
G
(
x
)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 1
85