Условия минимума этих функционалов, из которых следуют наи-
худшие оценки снизу значений
K
и
μ ,
имеют вид
δV
K
[
K, δK
] =
−
1
18
A
K
Z
V
1
K
2
K
R
K
V
K
−
1
−
−
K
V
1
−
K
R
K
δK σ
2
kk
dV
= 0
,
δV
μ
[
μ, δμ
] =
−
1
8
A
μ
Z
V
1
μ
2
μ
R
μ
V
μ
−
μ
V
1
−
μ
R
μ
δμ s
ij
s
ij
dV
= 0
,
откуда следуют неравенства
K
≥
2
K
R
K
V
K
V
+
K
R
, μ
≥
2
μ
R
μ
V
μ
V
+
μ
R
.
(
23
)
Достаточные условия существования минимумов функциона-
лов
V
K
[
K
]
и
V
μ
[
μ
]
выполняются, так как в окрестности минималь-
ных значений
K
и
μ
из соотношений (23) следуют неравенства
δ
2
V
K
[
K, δK
]
>
0
и
δ
2
V
μ
[
μ, δμ
]
>
0
.
Окончательно полученные результаты можно представить в виде
неравенств, объединяющих (22) и (23):
1
2
(
K
V
+
K
R
)
≥
K
≥
2
K
R
K
V
K
V
+
K
R
,
1
2
(
μ
V
+
μ
R
)
≥
μ
≥
2
μ
R
μ
V
μ
V
+
μ
R
.
(
24
)
Для проверки применимости неравенств (24) при оценке упру-
гих свойств двухкомпонентных сплавов было проведено сравнение
известных экспериментальных данных [15] по модулю упругости
E
= 9
Kμ/
(3
K
+
μ
)
сплава карбида вольфрама
(
K
1
= 419
ГПа,
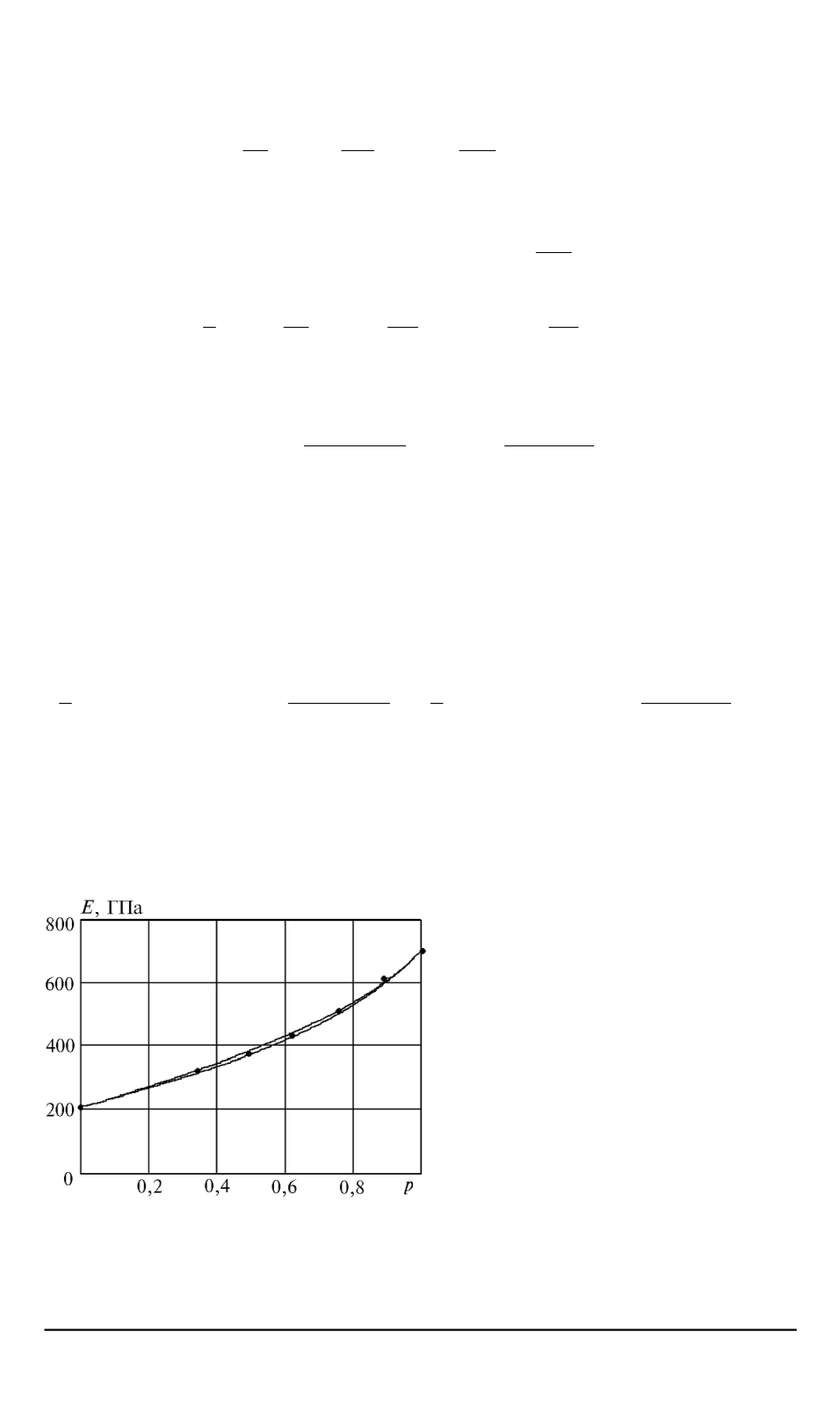
Рис. 1. Модуль Юнга для сплава карбида
вольфрама и кобальта
μ
1
= 288
ГПа) и кобальта
(
K
2
= 172
ГПа,
μ
2
= 79
,
3
ГПа).
На рис. 1 сплошные линии со-
ответствуют верхней и нижней
оценкам модуля упругости с ис-
пользованием неравенств (24),
точками отмечены эксперимен-
тальные данные. Видно, что
диапазон возможного измене-
ния модуля упругости достаточ-
но узок и соответствует экспе-
риментальным данным.
На рис. 2, 3 представлены ре-
зультаты расчета и границы ко-
эффициентов упругости
K
и
μ
74
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 1


