γ
(
n
+1)
f
=
γ
(
n
+1)
f
+ Δ
τ
n
η
(
n
)
−
γ
(
n
)
f
o
;
Γ
(
n
+1)
p
= Γ
(
n
)
p
+ Δ
τ
(
(1 +
γ
(
n
+1)
f
)
−
Γ
(
n
)
p
Ω
Θ
+
Q e
−
E
Γ
(
n
)
p
)
.
(28)
Здесь
n
— номер шага по времени; случайное приращение источ-
ника флуктуаций моделируется как
Δ
τη
(
n
)
=
ξ
(
n
)
p
2
h
η
2
i
τ
◦
Δ
τ
, где
ξ
(
n
)
— случайная реализация нормированного процесса Гаусса (бе-
лого шума) с нулевым средним значением и единичной дисперсией.
Шаг по времени в уравнениях (28) выбирается достаточно малым:
Δ
τ
= 10
−
2
min (1
,
Ω
Θ
)
. Сбор информации для получения осреднен-
ных параметров начинается со времени
τ >
10
2
max (1
,
Ω
Θ
)
.
Согласно уравнениям (27) и (28), при отсутствии тепловыделения
результаты аналитического исследования и результаты, полученные
путем осреднения численных реализаций системы (28), должны быть
близки.
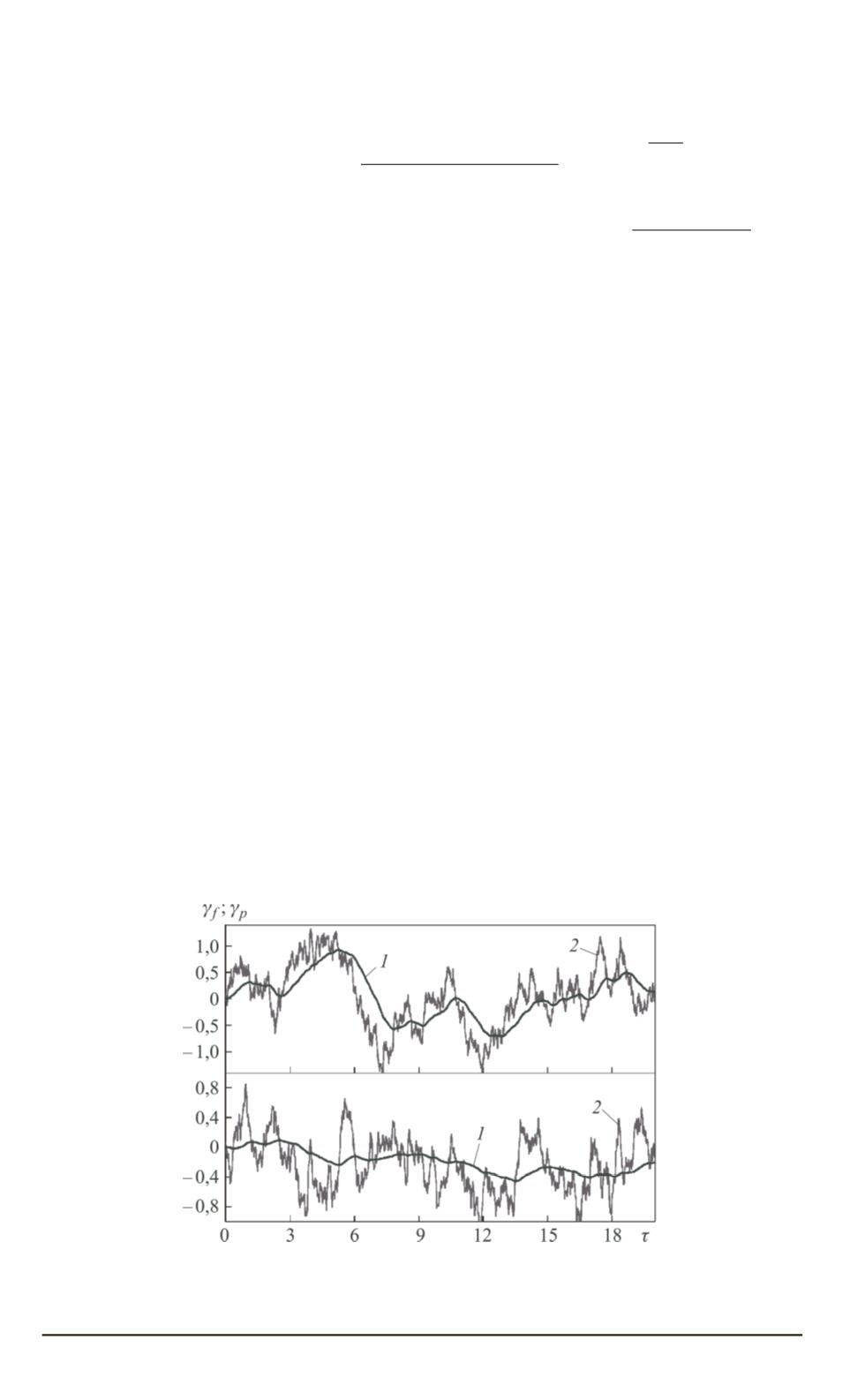
Влияние тепловой инерции гранул на характер флуктуаций темпе-
ратуры без тепловыделения иллюстрирует рис. 3. Увеличение тепло-
вой инерции приводит к снижению амплитуды флуктуаций и к их
более гладкому поведению.
На рис. 4 показано сопоставление результатов по относитель-
ной дисперсии флуктуаций температуры гранулы, полученных путем
осреднения данных имитационного моделирования системы (28) и по
аналитической формуле (23). Увеличение тепловой инерции понижает
интенсивность флуктуаций температуры гранул.
Автокорреляционные функции флуктуаций температуры части-
цы представлены на рис. 5. Результаты численного моделирования
удовлетворительно согласуются с точными данными, определенными
Рис. 3. Пример случайного поведения температуры среды и частиц при
Ω
θ
= 1
(
a
) и 3 (
б
) для
γ
p
(
1
) и
γ
f
(
2
)
14
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 2


