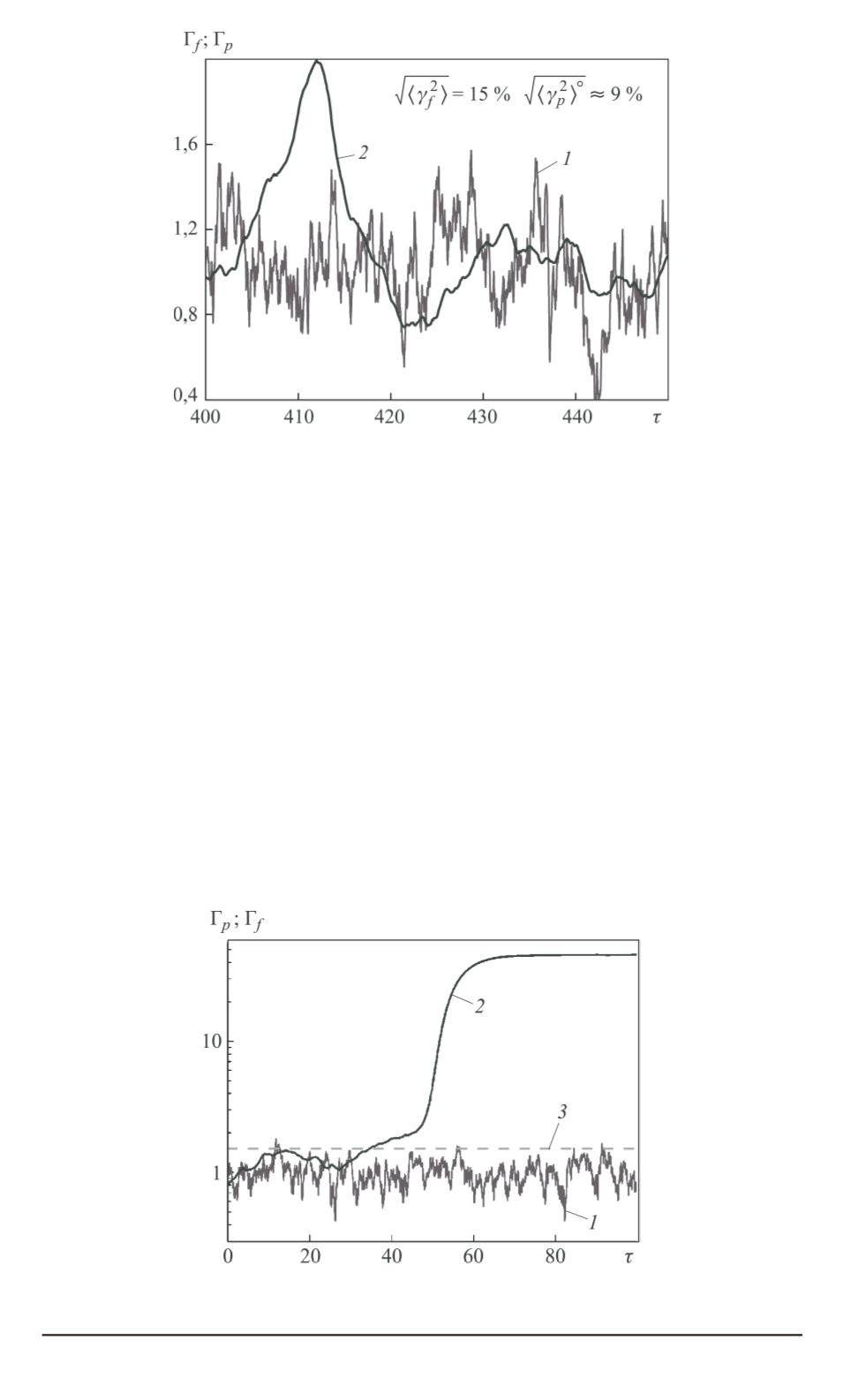
Рис. 6. Изменения актуальных температур среды
Γ
f
(
1
) и гранулы
Γ
p
(
2
) до
теплового взрыва (
γ
2
p
◦◦
p
— квадрат дисперсии флуктуаций температуры среды
без учета тепловыделения) при
Ω
Θ
= 2
потеря тепловой устойчивости. Этот сценарий проиллюстрирован на
рис. 7.
Время ожидания теплового взрыва определяем как среднее время
первого пересечения случайными флуктуациями температуры гранулы
критического уровня
Γ
cr
, среднее время ожидания теплового взрыва
τ
cr
в зависимости от начальной температуры гранулы
Γ
◦
p
, с которой
она подается во флуктуирующую среду, показано на рис. 8. По мере
приближения начальной температуры гранулы к критической среднее
время потери тепловой устойчивости резко сокращается. Критическая
температура зависит от параметра тепловой инерции гранулы.
Заключение.
Разработана процедура численного моделирования
случайной температуры гранулы с внутренним тепловыделением
Рис. 7. Пример возникновения теплового взрыва для
γ
f
(
1
),
γ
p
(
2
) и
Γ
II
(
3
)
при
Ω
Θ
= 4
16
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 2


