Рис. 4. Отношение дисперсий флуктуа-
ций температуры гранулы и среды по
результатам моделирования (
1
) и полу-
ченные по формуле (23) (
2
)
методом спектрального анализа
случайных процессов. Возраста-
ние тепловой инерции гранулы
увеличивает область затухания
автокорреляционной функции.
Сопоставление точных анали-
тических результатов и данных
численного эксперимента позво-
ляет утверждать об адекватности
предложенного в работе числен-
ного алгоритма моделирования,
основанного на решении системы
стохастических уравнений (28).
Моделирование теплового
взрыва. Среднее время ожи-
дания взрыва.
В этом разделе
приведены результаты, иллюстрирующие различные сценарии по-
ведения температуры частицы с внутренним тепловыделением во
флуктуирующей среде. Изменение актуальной температуры гранулы
с тепловыделением показано на рис. 6, где
Γ
f
= 1 +
γ
f
(
t
)
— акту-
альная температура среды. Флуктуации скорости химической реакции
вносят заметный вклад в случайную температуру гранулы. Начальная
температура гранулы меньше, чем критическое значение, соответству-
ющее второму корню
Γ
II
, взятому с диаграммы Семенова. Случайный
процесс с ненулевой вероятностью может выйти за любой уровень.
По истечении некоторого случайного времени актуальная температу-
ра частицы превысит критическое значение
Γ
cr
= Γ
II
и произойдет
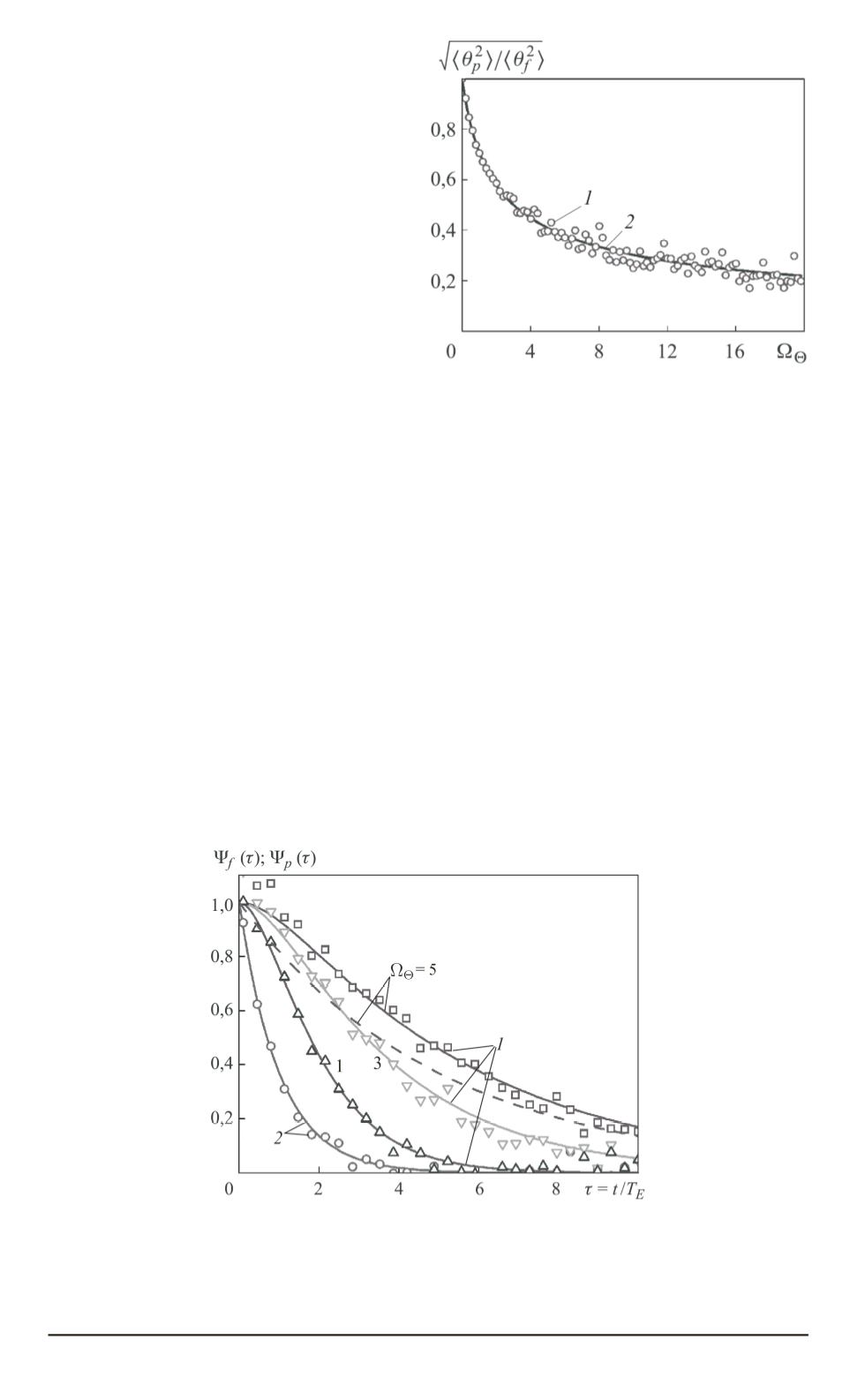
Рис. 5. Автокорреляционные функции флуктуаций температуры гранулы
(
1
) и среды (
2
) по результатам численного моделирования (
◦
,
Δ
,
O
,
), и
полученные по формулам (24) и (20) (кривые); штриховой линией показана
корреляционная функция (26)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 2
15


