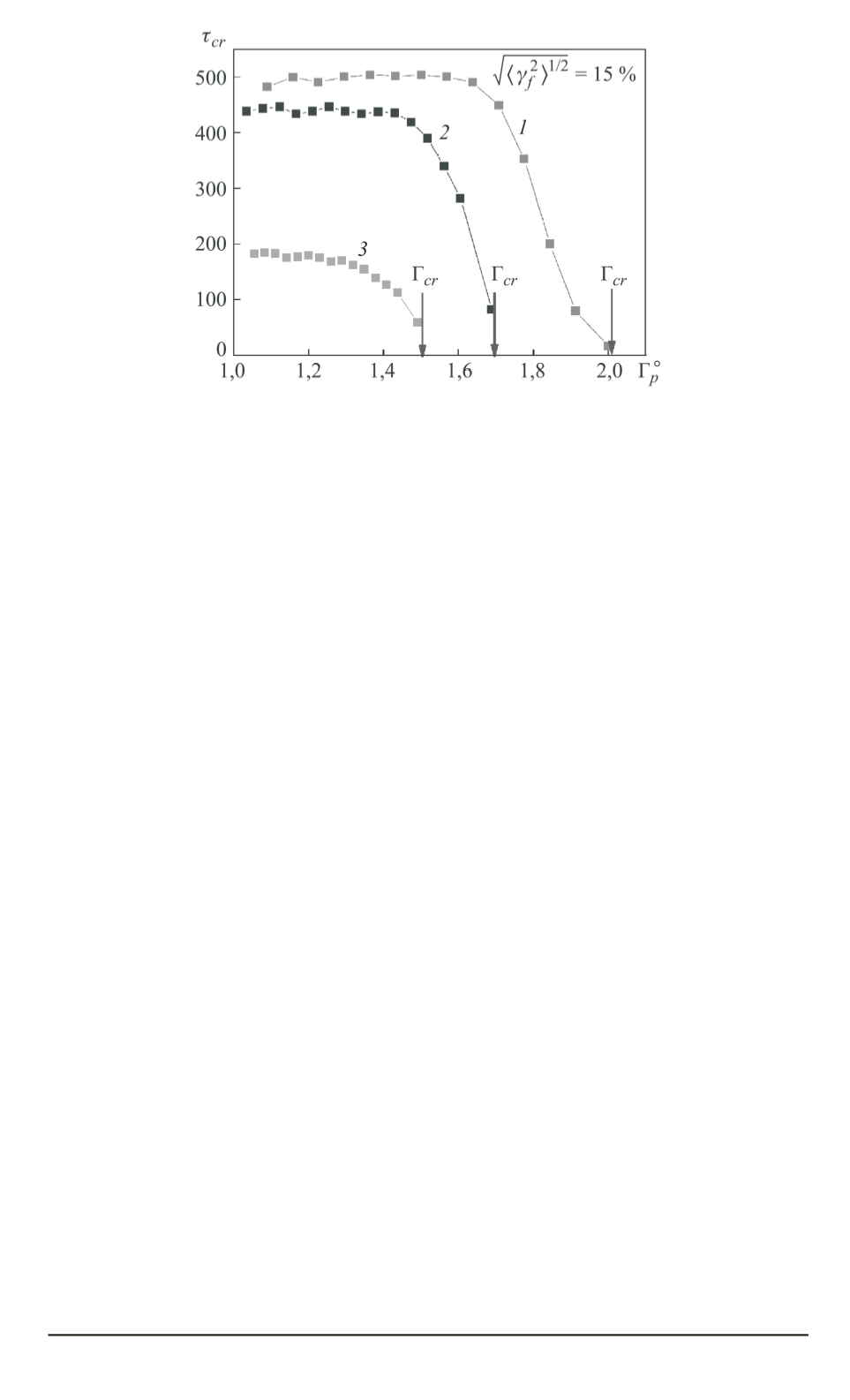
Рис. 8. Зависимость среднего времени ожидания теплового взрыва при
Ω
θ
= 1
(
1
), 1,5 (
2
) и 2 (
3
)
в жидкой среде с флуктуациями температуры. Интенсивность те-
пловыделения описывается законом Аррениуса.
Для флуктуаций температуры среды предложена процедура чи-
сленной генерации случайного процесса Гаусса с экспоненциально
затухающей автокорреляционной функцией. Автокорреляционные
функции и дисперсии флуктуаций температуры гранулы без тепловы-
деления, полученные методом имитационного моделирования, сопо-
ставляются с точными формулами, найденными путем спектрального
анализа случайных процессов.
Представлен анализ влияния флуктуаций температуры среды на
процесс возникновения теплового взрыва. Проиллюстрирована дина-
мика теплового взрыва для различных значений параметра тепловой
инерции начальной температуры частицы, уровня дисперсий темпе-
ратуры среды, мощности тепловыделений и энергии активации. На
основе осреднения данных имитационного моделирования установле-
на зависимость среднего времени ожидания начала теплового взрыва.
Обнаружен эффект стохастического дрейфа температуры частицы с
внутренним тепловыделением к ее критическому значению.
Направление дальнейших исследований в области численного мо-
делирования связано с привлечением в разработанный метод реальных
кинетических схем процесса синтеза Фишера – Тропша на кобальто-
вых катализаторах, а также исследования, посвященного учету пере-
межаемости, характеризуемой логарифмически нормальным законом
распределения случайной температуры среды.
Работа выполнена при финансовой поддержке Российского фонда
фундаментальных исследований (проект 11-08-00645-а).
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 2
17


