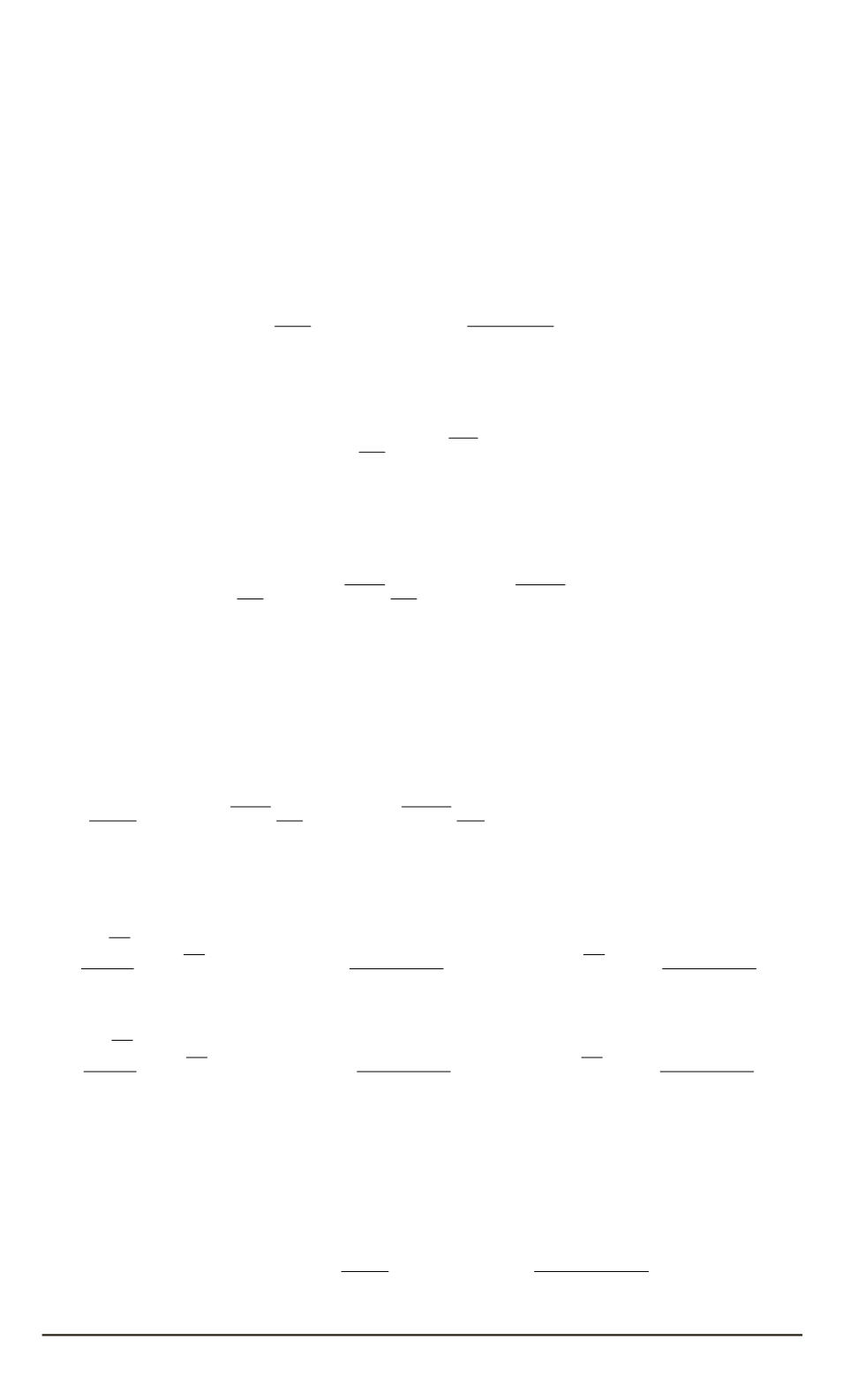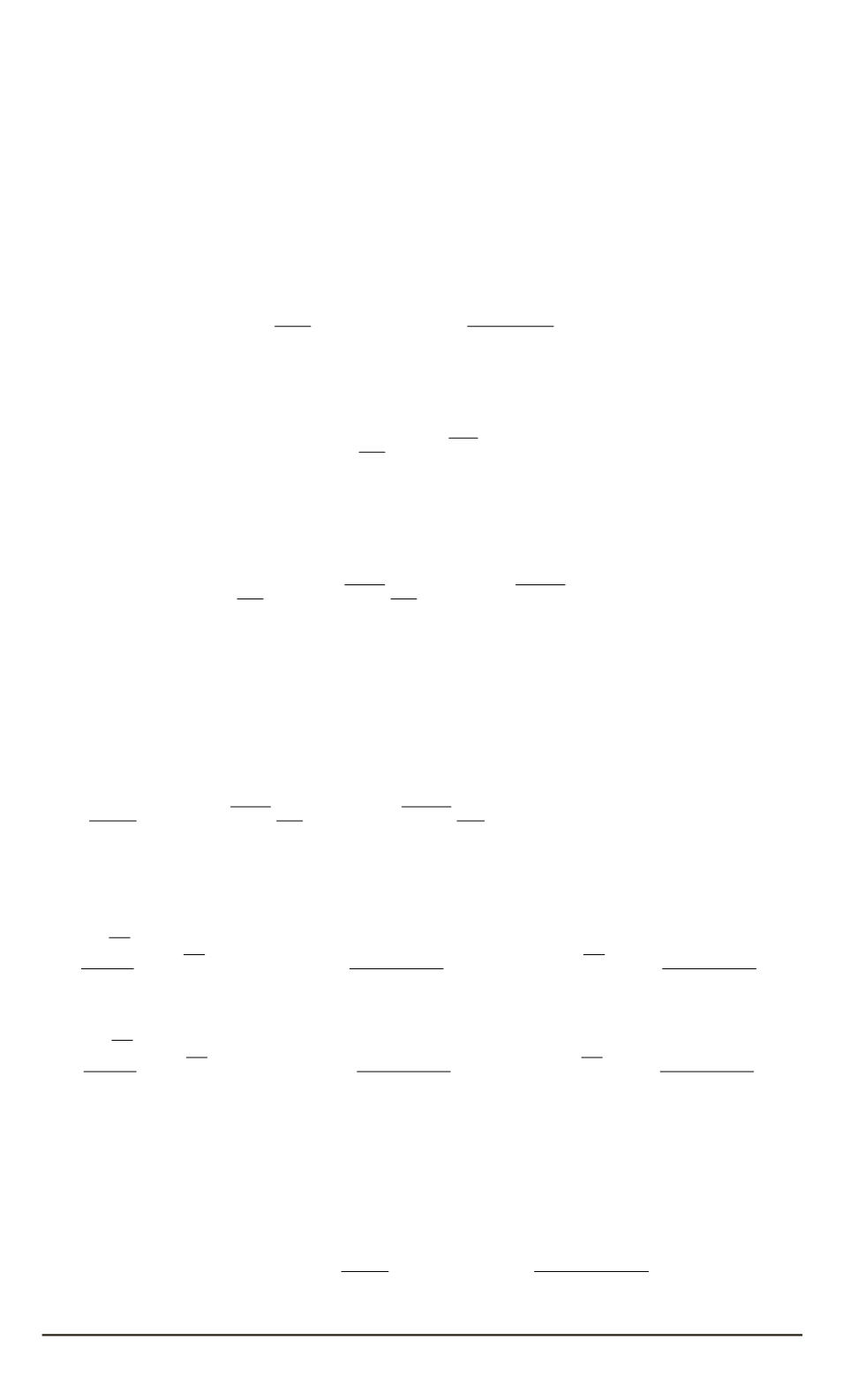
В соответствии с формулой (11) существование производной слу-
чайного процесса связано со сходимостью интеграла
∞
Z
−∞
ω
2
ψ
f
(
ω
)
dω.
Из формул (8) и (11) также следует представление для среднего ква-
драта производной случайного процесса через автокорреляционную
функцию
dθ
f
dt
2
=
−
θ
2
f
d
2
Ψ
f
(
t
)
dt
2
t
=0
.
Решение уравнения (3) с нулевым начальным условием имеет вид
θ
p
(
t
) =
1
τ
Θ
t
Z
0
e
−
t
−
s
τ
Θ
θ
f
(
s
)
ds.
Двухвременн´ая корреляция флуктуаций температуры гранулы равна
h
θ
p
(
t
0
)
θ
p
(
t
00
)
i
=
1
τ
Θ
t
0
Z
0
ds
0
e
−
t
0
−
s
0
τ
Θ
1
τ
Θ
t
00
Z
0
ds
00
e
−
t
00
−
s
00
τ
Θ
h
θ
f
(
s
0
)
θ
f
(
s
00
)
i
.
(12)
Корреляцию флуктуаций температуры среды в формуле (12) пред-
ставляем в спектральном виде (8):
h
θ
p
(
t
0
)
θ
p
(
t
00
)
i
=
=
θ
2
f
τ
Θ
t
0
Z
0
ds
0
e
−
t
0
−
s
0
τ
Θ
1
τ
Θ
t
00
Z
0
ds
00
e
−
t
00
−
s
00
τ
Θ
1
2
π
∞
Z
−∞
dωe
−
iω
(
s
0
−
s
00
)
ψ
f
(
ω
)
.
(13)
Интегралы в формуле (13) вычисляются в предположении
t τ
Θ
:
e
−
t
0
τ
Θ
τ
Θ
t
0
Z
0
e
s
0
τ
Θ
(1
−
iωτ
Θ
)
ds
0
=
1
1
−
iωτ
Θ
e
−
iωt
0
−
e
−
t
0
τ
Θ
=
e
−
iωt
0
1
−
iωτ
Θ
;
e
−
t
00
τ
Θ
τ
Θ
t
00
Z
0
e
s
00
τ
Θ
(1+
iωτ
Θ
)
ds
00
=
1
1 +
iωτ
Θ
e
iωt
00
−
e
−
t
00
τ
Θ
=
e
iωt
00
1 +
iωτ
Θ
.
Подставим эти формулы в выражение (13) и найдем связь между
спектром флуктуаций температуры среды и корреляционной функцией
флуктуаций температуры гранулы
h
θ
p
(
t
0
)
θ
p
(
t
00
)
i
=
θ
2
f
2
π
∞
Z
−∞
e
−
iω
(
t
0
−
t
00
)
ψ
f
(
ω
)
1 + (
ωτ
Θ
)
2
dω.
(14)
10
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 2