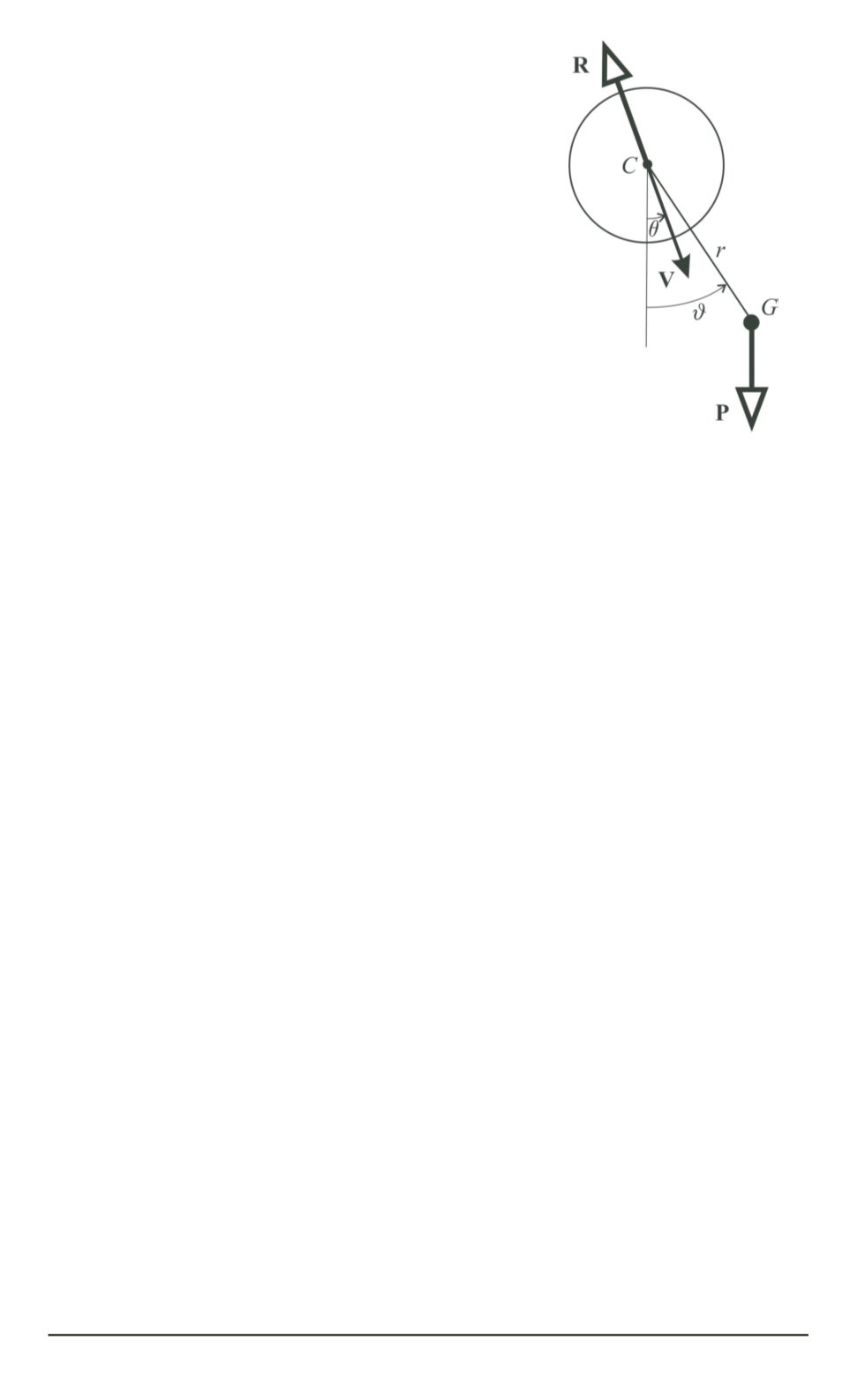
Рис. 1. Схема, иллюстриру-
ющая важность предполо-
жения Жуковского
оболочку), имеющее конечные размеры, но
масса которого сосредоточена в одной точ-
ке
G
. При этом ориентация оболочки отно-
сительно вектора скорости точки
G
должна
быть такой, чтобы момент аэродинамиче-
ских сил, действующих на оболочку, был
равен нулю. В дальнейшем соответствую-
щий угол атаки получил название “баланси-
ровочный угол атаки”. Это понятие широко
используется в прикладных задачах дина-
мики летательных аппаратов (ЛА) вплоть
до моделирования спуска отделяющихся
частей космических ракет-носителей [3].
В частности, оно упоминалось в некото-
рых докладах на 7 Международном аэро-
космическом конгрессе, который состоялся
в Москве в 2012 г. При этом обычно мало
внимания обращают на дополнительное предположение Н.Е. Жуков-
ского:
близость центра тяжести к центру давления.
Продемонстри-
руем важность этого предположения на простой задаче.
Пусть оболочка (рис. 1) представляет собой шар с центром
С
. При-
мем, что при ее движении в среде точка
С
является центром давления,
а центр масс тела отстоит от точки
С
на расстояние
r
. На тело дей-
ствуют сила тяжести
Р
(
P
=
mg
) и сила сопротивления среды
R
,
направленная против вектора скорости
V
точки
С
(
R
=
dV
2
, где
d
—
постоянный коэффициент лобового сопротивления).
Очевидно, что тело может совершать прямолинейный спуск, при
котором вектор скорости
V
и ось
CG
ориентированы вертикально,
причем точка
G
расположена ниже точки
С
(как при спуске на пара-
шюте). Скорость стационарного спуска
V
определяется по формуле
dV
2
=
mg
.
Для простоты ограничимся рассмотрением случая плоскопарал-
лельного движения тела. Введем возмущение скорости
v
=
V
−
V
и углы
θ, ϑ
отклонения от вертикали вектора скорости
V
и оси
CG
,
запишем уравнения возмущенного движения тела в линейном прибли-
жении
m
˙
v
=
−
2
dV v
;
(1)
m
(
r
¨
ϑ
+
V
˙
θ
) =
−
dV
2
θ
;
J
¨
ϑ
=
−
rdV
2
(
ϑ
−
θ
)
,
(2)
где
J
— центральный момент инерции тела.
Уравнение (1) имеет тот же вид, что и уравнение для вертикального
спуска материальной точки в классической задаче внешней баллисти-
ки. Уравнение (2) при
J
→
0
(невесомая оболочка, безынерционный
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 2
33


