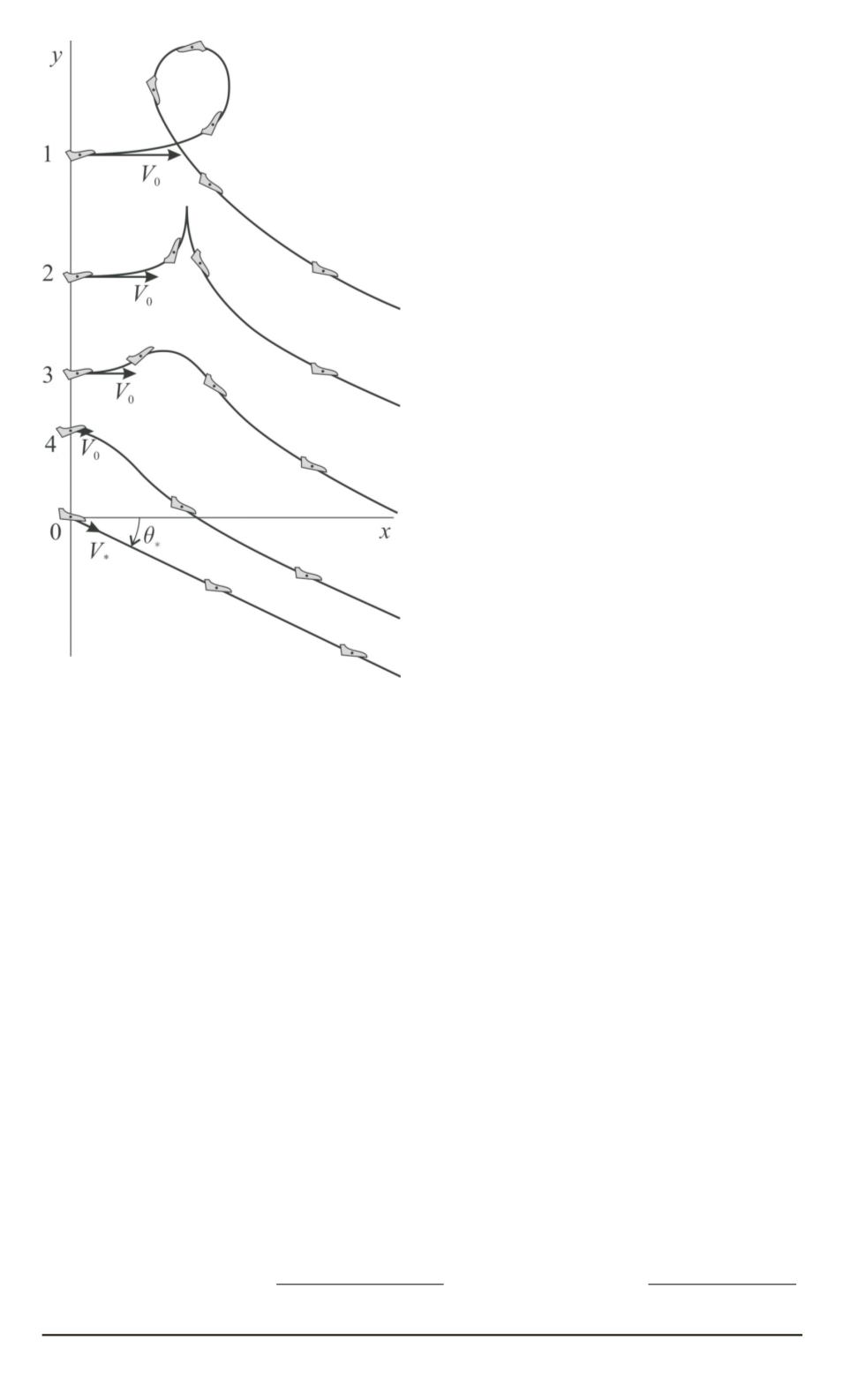
Рис. 5. Траектории движения
причем переход сопровождается
предварительным подъемом точ-
ки
G
(маневр типа “горка”, тра-
ектории 2 и 3, см. рис. 5). При
еще меньших скоростях происхо-
дит “провал” точки
G
и плав-
ный выход на режим планирования
(траектория 4, см. рис. 5). Отметим,
что все траектории, приведенные
на рис. 5, известны: это характер-
ные траектории полета бумажного
“голубя”, включая зачастую наблю-
даемое “кабрирование”.
Теперь учтем влияние силы тя-
ги в присутствии всего набора ука-
занных выше сил. Имея в виду
модификацию задачи Жуковского
о полете планера, будем полагать,
что сила тяги постоянна (
T >
0
), а
масса точки неизменна.
Для дальнейшего анализа пе-
рейдем к безразмерным величи-
нам, выполнив следующие замены:
V
=
V v
;
t
=
V τ/g
;
T
=
pmg
(
p
≥
0
). Учитывая связь значений
θ
и
K
, получаем
v
0
=
p
+
v
2
sin
θ
−
sin
θ
;
vθ
0
=
v
2
cos
θ
−
cos
θ.
(6)
Система (6) включает в себя два параметра:
p
и
θ
(или
K
, так
как они связаны однозначной зависимостью). Естественно, фазовый
портрет системы будет зависеть от значений этих параметров. Легко
показать, что при
0
≤
p <
1
существует единственный режим планиро-
вания, который является непрерывным продолжением режима плани-
рования при нулевой силе тяги. Ему соответствует неподвижная точка
А
на фазовой плоскости. При
1
≤
p <
1
/
cos
θ
имеются два режима:
один — продолжение предыдущего, другой — возникающий из режи-
ма “зависания”, когда сила тяги уравновешивает силу тяжести (точка
В
на фазовой плоскости). При
p
= 1
/
cos
θ
два режима сливаются в
один. Наконец, при дальнейшем увеличении силы тяги (
p >
1
/
cos
θ
)
стационарные режимы отсутствуют.
Последний случай особенно интересен. Из уравнений (6) следует,
что
v
0
<
0
при
v
≤
p
−
(1 +
p
)
/
sin
θ
,
v
0
>
0
при
v
≥
p
(1
−
p
)
/
sin
θ
.
38
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 2


