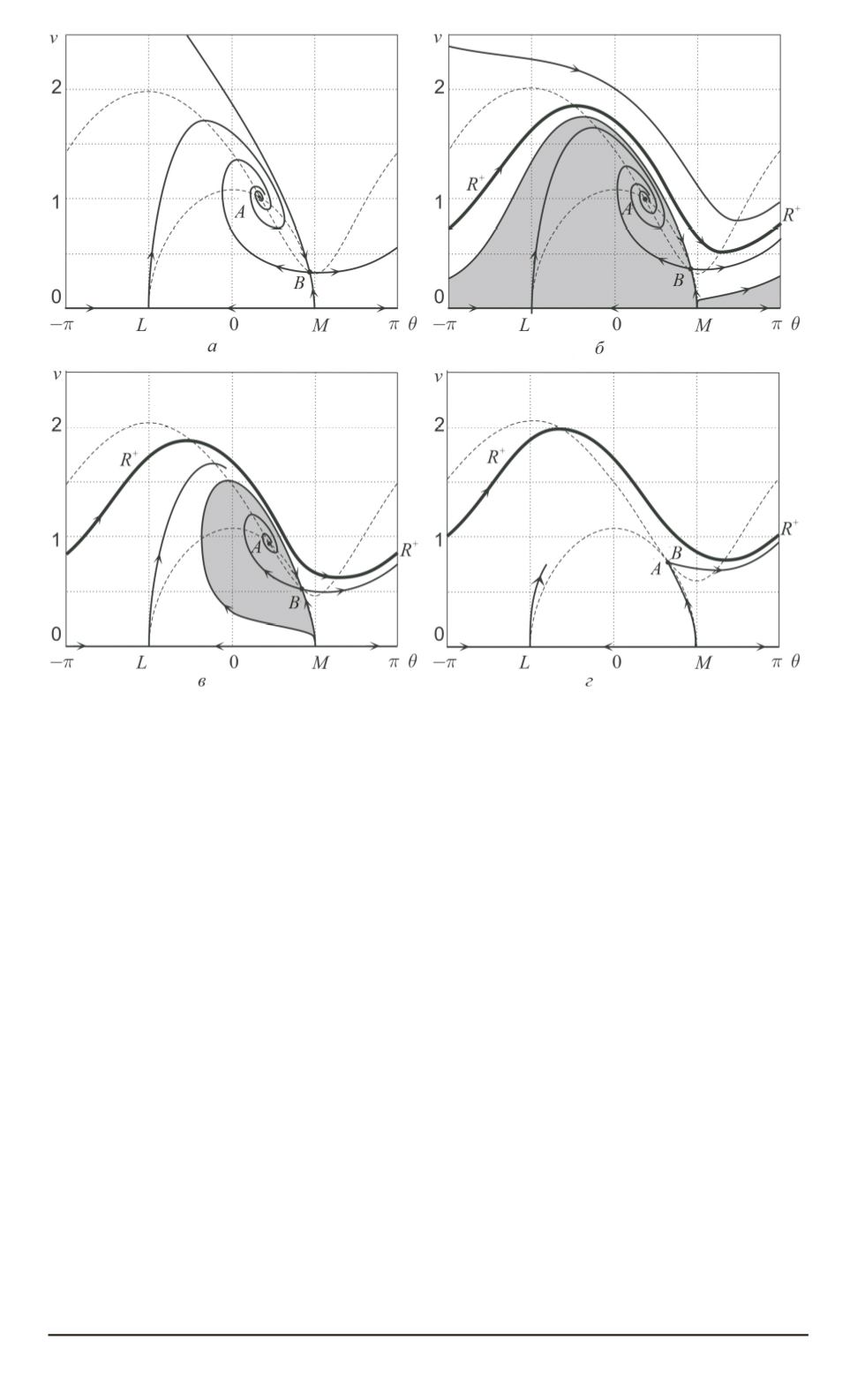
Рис. 7. Фазовый портрет системы (5) при
p
= 1
,
04
(
a
), 1,092 (
б
), 1,11 (
в
) и 1,179 (
г
)
цикл, он ограничивает область притяжения точки
А
. Часть фазовой
плоскости, расположенная снаружи этого цикла, образует область при-
тяжения режима
R
+
. При дальнейшем увеличении значения
p
данный
цикл сжимается и при
p
=
p
S
= 1
,
1713
исчезает, точка
А
становится
неустойчивым фокусом (классический случай бифуркации Андроно-
ва – Хопфа), и в диапазоне значений
p
S
< p < p
max
неподвижные точ-
ки неустойчивы, существует только один аттрактор
R
+
. При
p
=
p
max
точки
А
и
В
совпадают (см. рис. 7,
г
), а затем при
p > p
max
исчезают,
остается только один устойчивый ротационный режим.
Итак, установлено, что в задаче Жуковского при наличии посто-
янной силы тяги в зависимости от значений силы тяги
p
и аэродина-
мического качества
K
возможны два типа притягивающих движений
материальной точки
G
: планирование с постоянными значениями ско-
рости и угла планирования; петлеобразное движение с периодически
изменяющейся скоростью движения и монотонным возрастанием угла
поворота вектора скорости точки
G
.
Режим планирования качественно не отличается от классического
случая отсутствия силы тяги. Отметим только, что он устойчив не обя-
зательно в большом и при достаточно больших значениях силы тяги
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 2
41


