угол планирования может быть равен нулю (горизонтальный полет)
и даже может быть положительным, так что точка
G
в этом случае
совершает стационарное движение с набором высоты.
Более сложная ситуация с петлеобразными движениями. Предста-
вляет интерес оценить “размах” петель, которые описывает точка
G
в
этом режиме, и средний “дрейф” траектории точки
G
в вертикальной
плоскости. Поскольку угол
θ
монотонно возрастает в данном устано-
вившемся режиме, можно перейти к новому “времени” — углу и искать
решение уравнений в виде функций этого угла. Пусть
ξ, η
— горизон-
тальное и вертикальное безразмерные смещения точки
G
в плоскости
движения и
w
=
v
2
. Ограничиваясь первыми членами разложения в
ряд Фурье, получаем первую грубую оценку изменения скорости дви-
жения точки
G
и ее траектории движения:
w
=
v
2
=
p
√
1 +
K
2
−
4
√
1 +
K
2
4 +
K
2
sin
θ
+
2
K
√
1 +
K
2
4 +
K
2
cos
θ.
(7)
Согласно (7), с увеличением силы тяги среднее значение скорости
движения точки
G
возрастает как
√
p
, а “амплитуда” изменения ско-
рости движения в этом приближении не зависит от силы тяги
p
. Ана-
логичные формулы могут быть записаны и для координат:
ξ
=
a
1
θ
+
+
b
1
sin
θ
+
c
1
cos
θ
;
η
=
a
2
θ
+
b
2
sin
θ
+
c
2
cos
θ
. Определенные при-
ближения для описания петлеобразных траекторий движения точки
G
становятся более точными с увеличением силы тяги.
Для иллюстрации рассмотрим результаты численного расчета тра-
екторий точки
G
в вертикальной плоскости при различных значени-
ях силы тяги и фиксированном значении аэродинамического качества
K
= 1
,
6
(рис. 8).
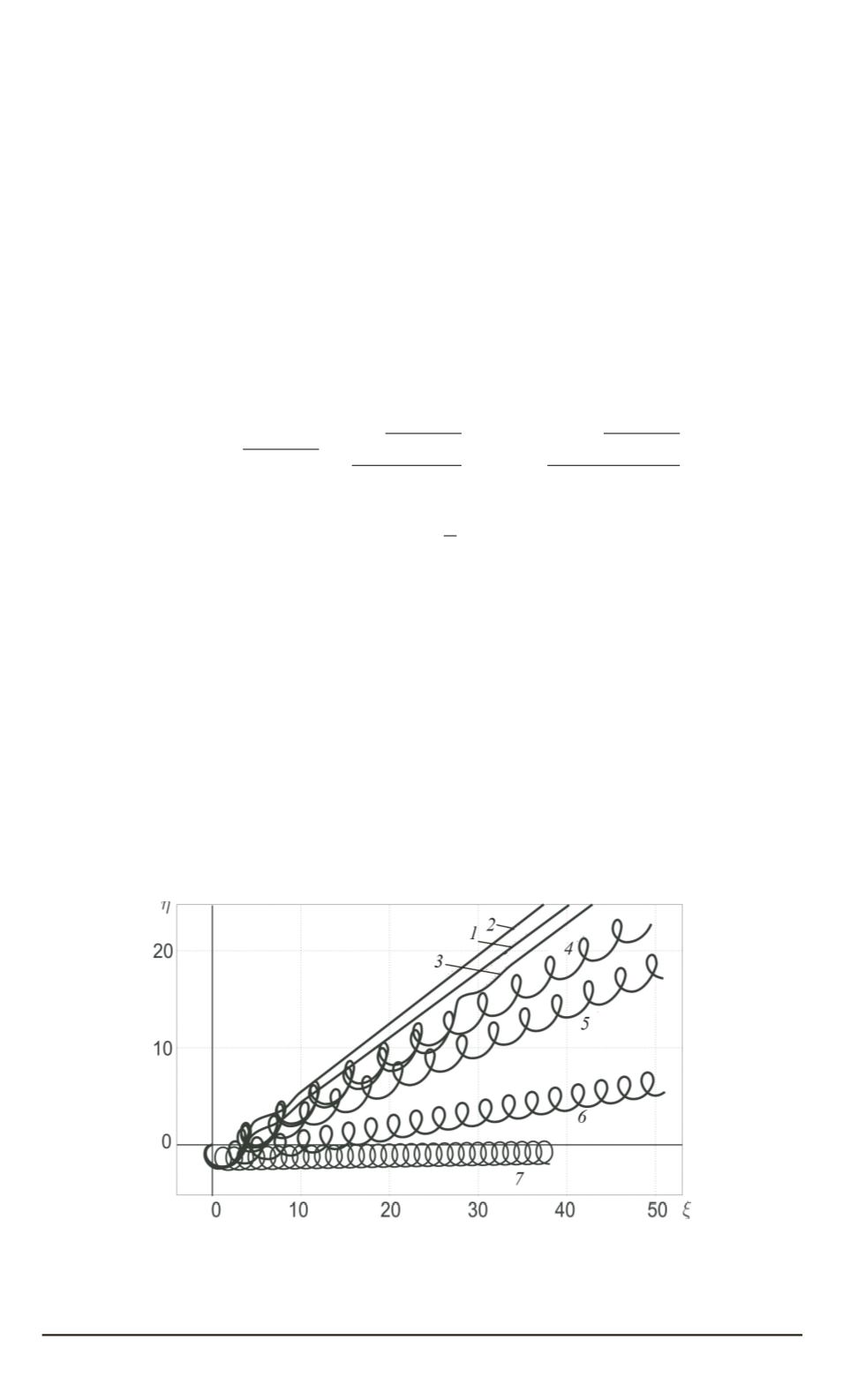
Рисунок наглядно демонстрирует, как с увеличением силы тяги
начинает развиваться петлеобразное движение точки
G
, при этом в
Рис. 8. Результаты численного расчета траекторий точки
G
в вертикальной
плоскости при значениях силы тяги
p
= 1
,
08
(
1
), 1,09 (
2
), 1,0905 (
3
), 1,0907
(
4
), 1,095 (
5
), 1,20 (
6
) и 2,20 (
7
) и фиксированном значении аэродинамического
качества
K
= 1
,
6
42
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 2


