парашют и т.п.) дает соотношение
ϑ
(
t
) =
θ
(
t
)
. Это означает, что так
называемый балансировочный угол атаки равен нулю. С учетом этого
уравнение (1) принимает вид
r
¨
ϑ
+
V
˙
ϑ
+
gϑ
= 0
,
(3)
аналогичный виду уравнения малых колебаний математического ма-
ятника длиной
r
, на который действует сила вязкого трения с коэф-
фициентом
V
. Очевидно, что при достаточно малой скорости спуска
или достаточно большом значении
r
(
V
2
<
4
rg
) ось
CG
тела соверша-
ет медленно затухающие угловые колебания. Именно такие колебания
нередко совершает тело, спускаемое на парашюте с длинными стро-
пами. Однако при достаточно малом (но конечном) значении
r
угол
ϑ
убывает монотонно, а при
r
→
0
уравнение (3) превращается в
уравнение, описывающее изменение угла поворота вектора скорости
падающей материальной точки. Таким образом, в этой задаче имеются
два параметра
J
и
r
, малость которых и учел Жуковский.
Задача о спуске тела на малом парашюте.
В следующей задаче
влияние длины строп на характер колебаний спускаемого объекта про-
является более ярко. Рассмотрим плоскопараллельное движение грузо-
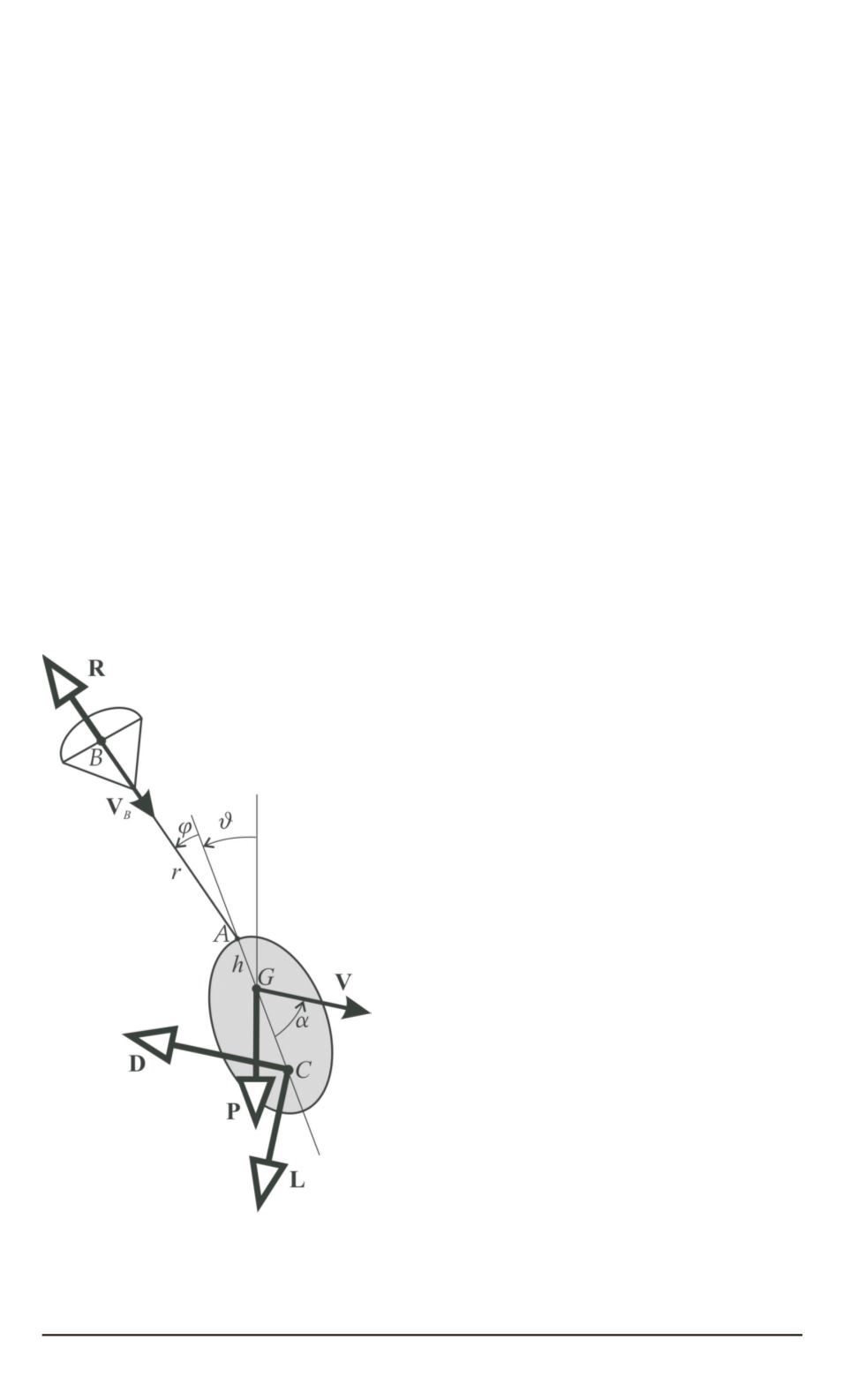
парашютной системы (рис. 2), состоящей из груза (осесимметричное
Рис. 2. Схема плоскопараллельно-
го движения грузопарашютной си-
стемы
тело) и малого безынерционного осе-
симметричного парашюта неизменя-
емой формы (масса парашюта и
масса воздуха под куполом много
меньше массы груза). Типичное на-
значение малых парашютов — обес-
печение желательной ориентации гру-
зов продолговатой формы при их
спуске. Известно, что такие грузы
имеют тенденцию к спуску в гори-
зонтальном положении, в то время
как желательным режимом является
спуск в вертикальном положении.
При исследовании систем с малым
(невесомым) парашютом традицион-
но используется эвристическая мо-
дель, в которой парашют заменяется
его аэродинамической силой, прило-
женной в точке крепления к грузу,
причем эта сила (в случае нулевого
балансировочного угла атаки) напра-
влена против воздушной скорости ха-
рактерной точки груза: центра масс
34
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 2


