в работах [4–6], предельным переходом
r
→
0
(при нулевой эффек-
тивной длине строп). Однако в этом случае требуется существенный
пересмотр модели аэродинамического воздействия на парашют.
Исследуем влияние эффективной длины строп на поведение систе-
мы. Нетрудно показать, что при выполнении условий
σhC
R
+
C
α
m
>
0;
C
α
m
<
0;
C
α
L
>
0
вертикальный спуск асимптотически устойчив при малых значениях
r
и неустойчив при больших.
Чтобы проанализировать влияние эффективной длины строп
r
на
характер колебаний в окрестности стационарного режима, были про-
ведены численные расчеты при следующих значениях параметров:
m
= 10;
h
= 0
,
5;
σ
≈
4
,
5;
C
L
(
α
) = sin 2
α
;
C
D
(
α
) = 0
,
5 + 2 sin
2
α
;
C
m
(
α
) = (
−
0
,
1 + 0
,
25 cos
α
) (
C
L
(
α
) cos
α
+
C
D
(
α
) sin
α
) ;
C
R
= 1
,
0
.
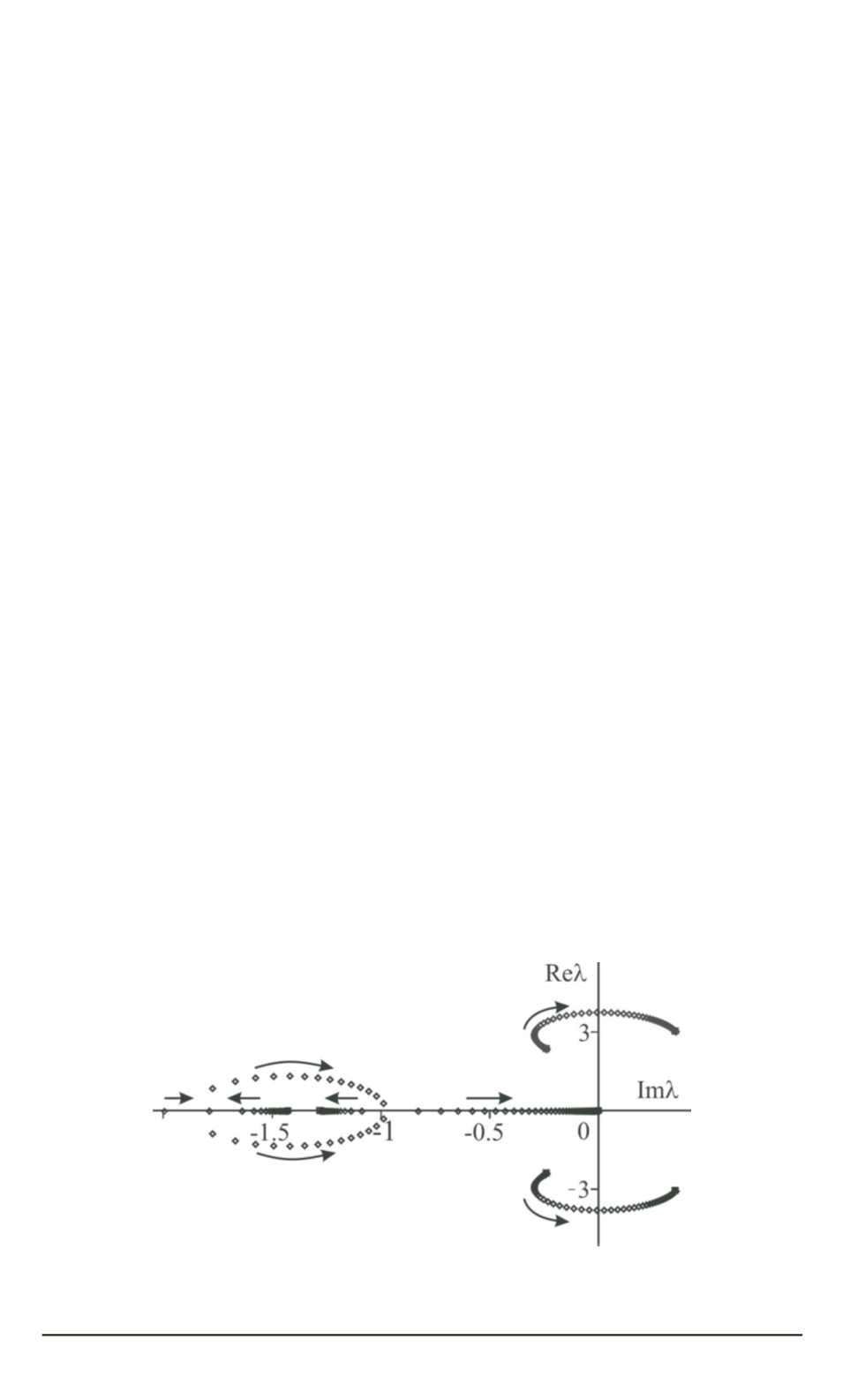
Траектории корней характеристического уравнения системы (4)
при изменении длины
r
приведены на рис. 3. Согласно рисунку, ча-
стота затухающих колебаний заметно изменяется в диапазоне отно-
сительно малых значений
r
и остается постоянной при достаточно
больших значениях длины
r
.
Интересно также, что в некотором диапазоне значений
r
суще-
ствует две частоты колебаний (при определенных соотношениях на
остальные параметры), причем низкая частота всегда соответствует
затухающим колебаниям, а высокая – может соответствовать раскач-
ке. Таким образом, эффективная длина строп оказывает существенное
влияние на характер колебаний в окрестности вертикального спуска
системы, вплоть до потери его устойчивости.
Задача Жуковского.
Задача о продольном полете ЛА (птицы, пла-
нера) [1] обсуждается в литературе, посвященной нелинейным дина-
мическим системам [8, 9], под названием “задача Жуковского”. При
Рис. 3. Траектории корней характеристического уравнения системы (4) при из-
менении длины
r
(стрелками отмечены направления увеличения длины строп)
36
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 2


