Таким образом, изображающая точка в процессе движения вдоль фазо-
вой траектории обязательно попадет в полосу
p
(1
−
p
)
/
sin
θ < v <
<
p
−
(1 +
p
)
/
sin
θ
и ее не покинет. В этом случае обязательно возни-
кает хотя бы одна (или нечетное число) замкнутая фазовая траектория,
охватывающая фазовый цилиндр (ротационное движение изображаю-
щей точки).
Рассмотрим вопрос об устойчивости режимов планирования (не-
подвижных точек). Несложно показать, что точка
В
— седловая,
поэтому соответствующий режим планирования неустойчив. Усло-
вие устойчивости точки
А
— единственное неравенство
p
(
K
2
−
2)
−
−
3
p
1 +
K
2
−
p
2
K
2
<
0
. Отсюда при
K
2
≤
2
условие устойчивости
точки
А
выполняется при всех допустимых значениях
p
силы тяги.
Если
K
2
>
2
, то условие устойчивости принимает вид
p <
3
/
√
K
2
+ 4
.
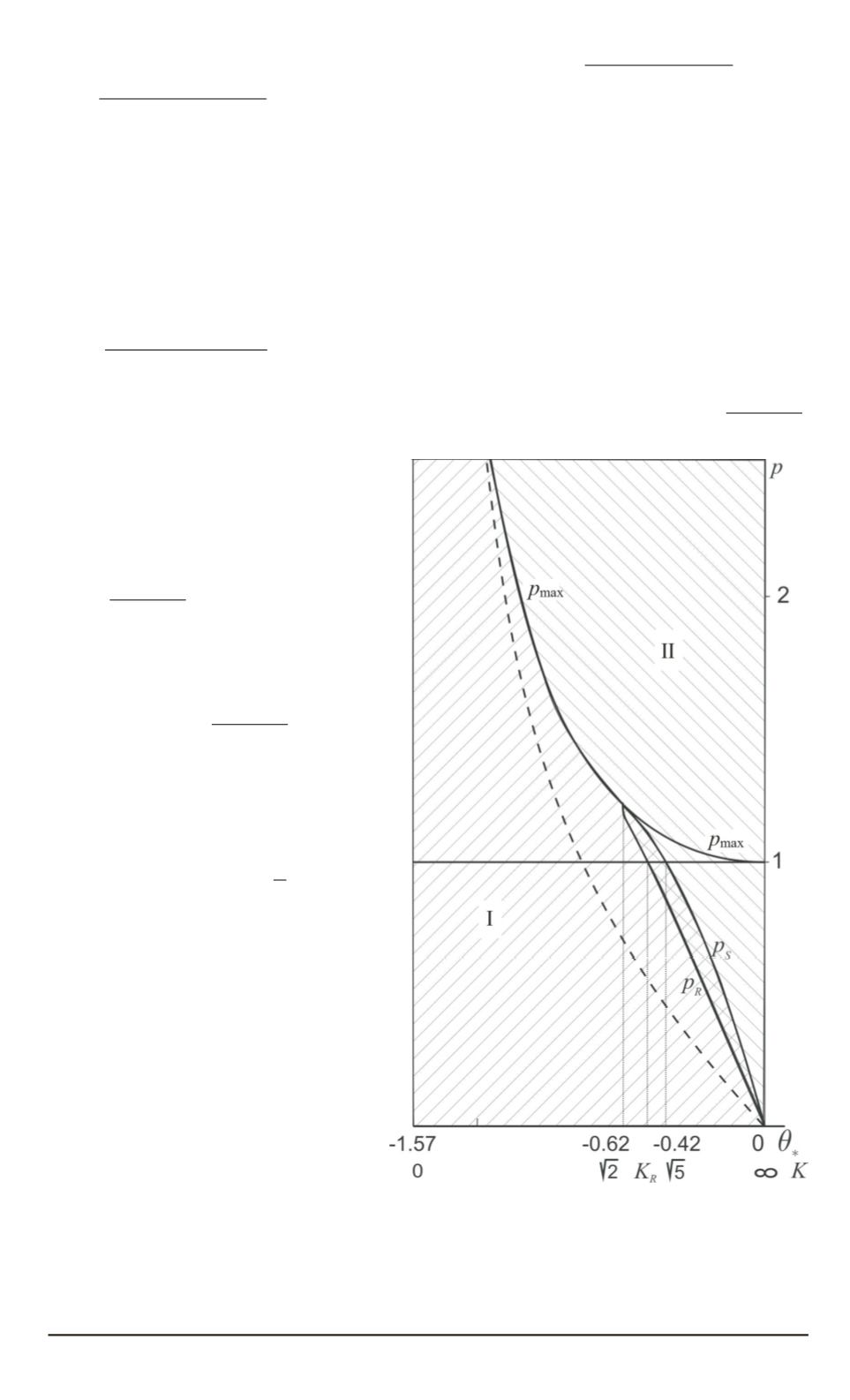
Рис. 6. Зависимость силы тяги от угла
θ
и
качества
K
:
I — область устойчивости точки
А
; II — область
существования притягивающего ротационного
режима
Переведем полученные ре-
зультаты на язык плос-
кости параметров
θ , p
(рис. 6). Введем две функ-
ции:
p
=
p
max
= 1
/
cos
θ
=
=
√
1 +
K
2
/K
— предель-
ное (максимальное) значение
силы тяги, до которого суще-
ствуют неподвижные точки;
p
=
p
S
= 3
/
√
K
2
+ 4
— гра-
ница области устойчивости
точки
А
при
K
2
>
2
. Отме-
тим, что кривые
p
max
(
K
)
и
p
S
(
K
)
имеют общую каса-
тельную при
K
=
√
2
. Таким
образом, в плоскости параме-
тров
θ , p
выделяются следу-
ющие множества (см. рис. 6):
0
≤
p <
1
— существует толь-
ко одна неподвижная точка
А
;
1
≤
p < p
max
— существу-
ют две неподвижные точки
А
и
В
; линия
p
=
p
max
— две
точки совпадают;
p > p
max
—
неподвижных точек нет. Кро-
ме того, кривая
p
=
p
S
делит
область
p
≤
p
max
существо-
вания неподвижных точек на
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 2
39


