деформированного состояния
,
независимо от числа управляющих па
-
раметров
,
при этом расчет градиентов производится без погрешностей
,
присущих методам численного дифференцирования
.
Таким образом
,
очевидно
,
что продолжительность расчета при применении метода
квадратичной аппроксимации без анализа чувствительности прибли
-
зительно в
15
и более раз превосходит продолжительность расчета при
применении метода проекции градиента в данной постановке зада
-
чи
.
Для параметризации диска при использовании метода проекции
градиента использовалась ломаная из
200
и более отрезков
,
при этом
продолжительность расчета была значительно меньше
,
чем при ис
-
пользовании квадратичной аппроксимации с
30
параметрами
.
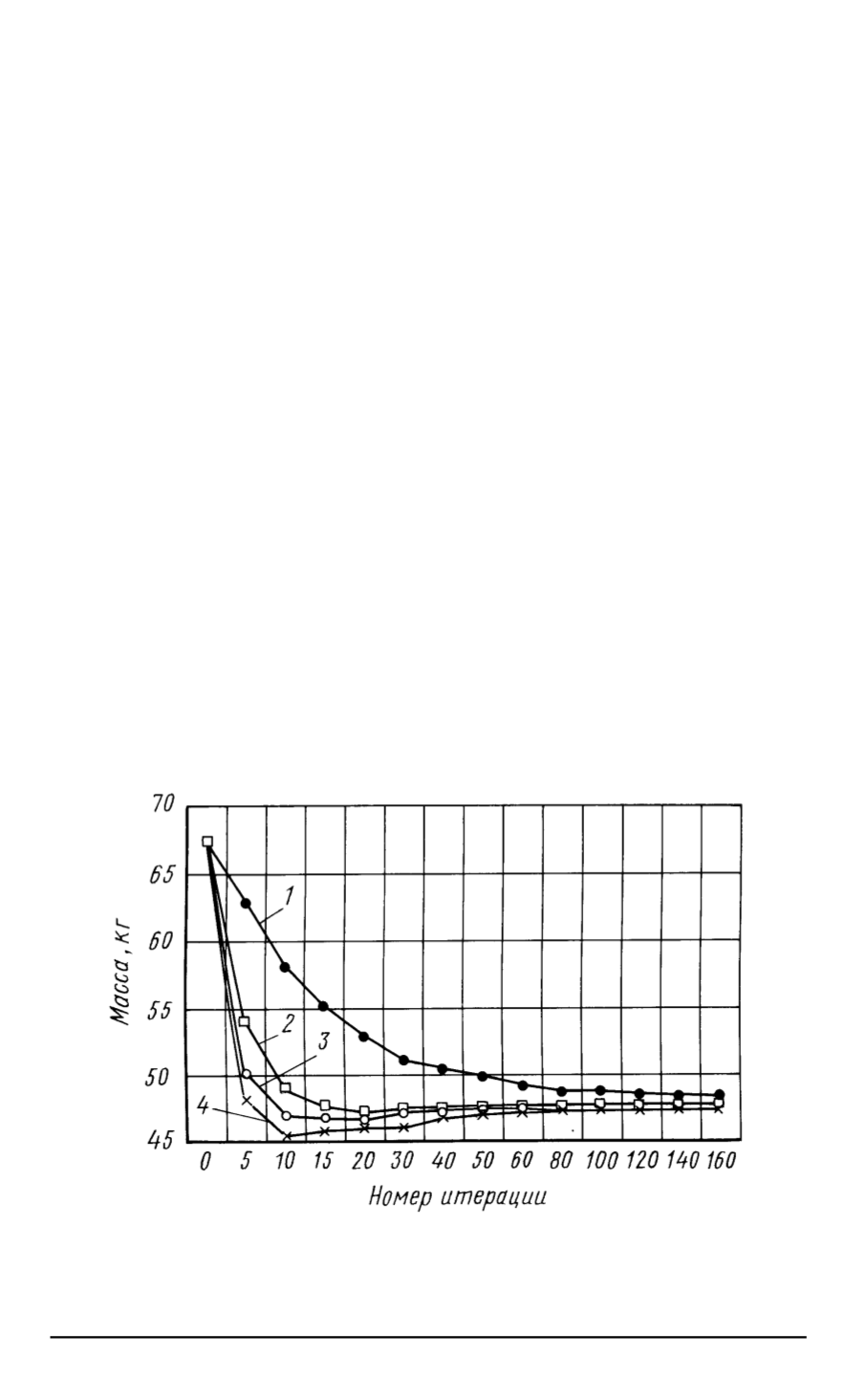
Из графиков изменения массы диска по итерациям
,
приведенных
на рис
. 8,
видно
,
что метод проекции градиента при решении данной
задачи имеет более высокую скорость сходимости по сравнению с ме
-
тодом квадратичной аппроксимации
.
Это объяснятся тем
,
что в реали
-
зованном методе проекции градиента величина шага выбиралась поль
-
зователем и в дальнейшем уменьшалась при необходимости
.
В мето
-
де квадратичной аппроксимации величина шага выбиралась из условия
минимума функции выигрыша
[6],
что обеспечивает более надежную
сходимость к истинному решению
,
но может приводить к вычислению
малых шагов в пространстве переменных проектирования
.
Таким образом
,
полуаналитический метод анализа чувствительно
-
сти позволяет существенно увеличить эффективность алгоритма опти
-
Рис
. 8.
Зависимость массы диска от итерации при использовании методов ква
-
дратичной аппроксимации
(
1
)
и проекции градиента с различными значениями
начального шага
(
2–4
) (
значение шага максимально для кривой
4
)
36
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2004.
№
2


