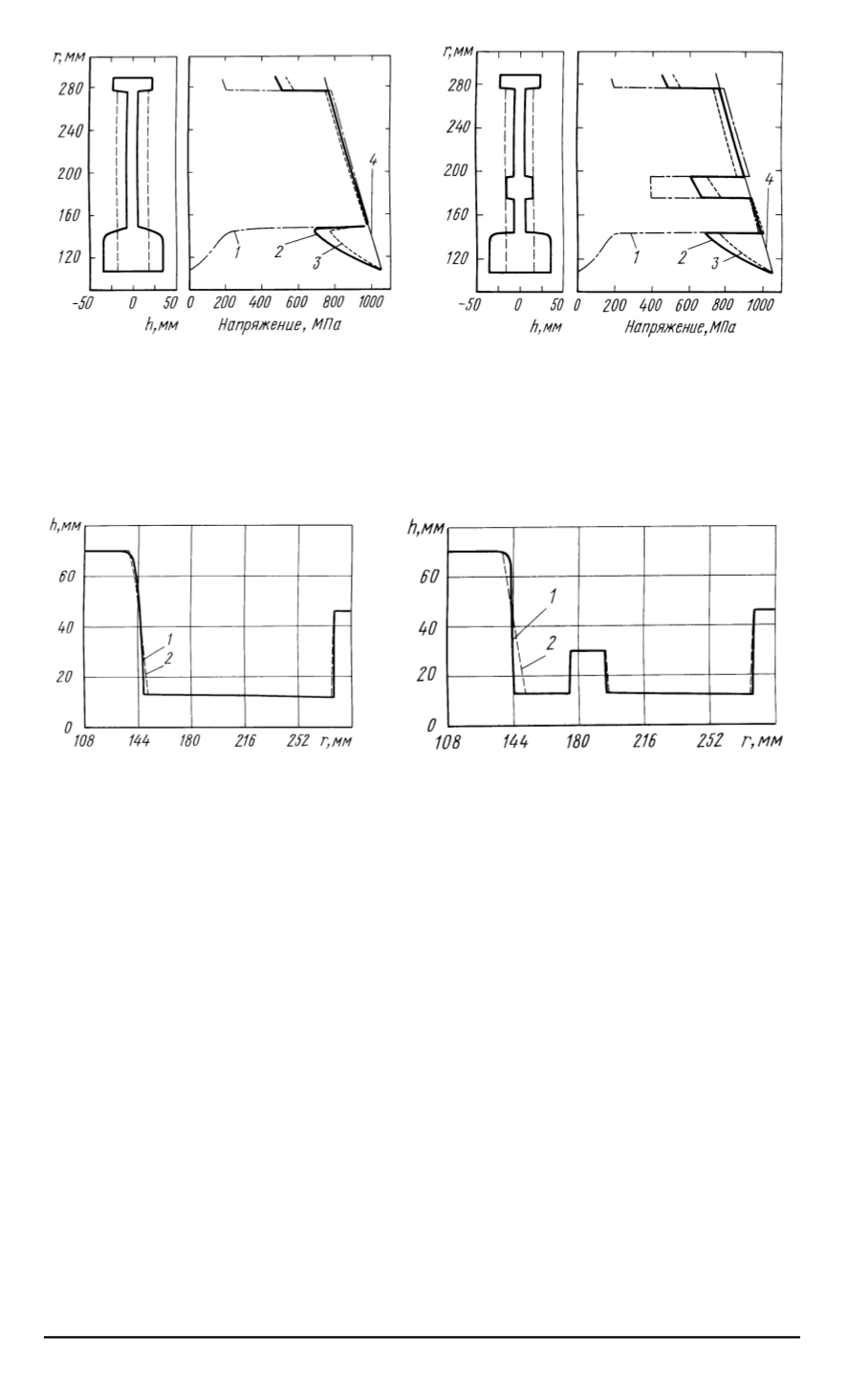
Рис
. 4.
Оптимизация диска методом
проекции градиента
:
1
—
σ
r
,
2
—
σ
i
,
3
—
σ
ϑ
,
4
— [
σ
]
Рис
. 5.
Оптимизация диска с дополни
-
тельным конструктивным ограниче
-
нием методом проекции градиента
:
1
—
σ
r
,
2
—
σ
i
,
3
—
σ
ϑ
,
4
— [
σ
]
Рис
. 6.
Оптимальный проект дис
-
ка
,
полученный методами проек
-
ции градиента
(
1
)
и квадратич
-
ной аппроксимации
(
2
)
Рис
. 7.
Оптимальный проект диска с до
-
полнительным конструктивным ограни
-
чением
,
полученный методами проекции
градиента
(
1
)
и квадратичной аппрокси
-
мации
(
2
)
Решение задачи профилирования диска методом проекции гради
-
ента
(25)
и методом квадратичной аппроксимации показало
,
что ре
-
зультаты расчетов незначительно отличаются как по массе
,
так и по
форме конструкции
(
рис
. 6, 7).
Однако следует заметить
,
что примене
-
ние полуаналитического анализа чувствительности проекта позволило
значительно сократить продолжительность расчета
.
При применении
метода квадратичной аппроксимации использовалась параметризация
диска в виде ломаной из
30
отрезков
.
Это привело к необходимости
проводить расчет конструкции
30
раз для вычисления градиентов на
каждой итерации
.
Таким образом
,
продолжительность расчета в этом
случае существенно зависела от числа управляющих параметров
.
В
методе проекции градиента с полуаналитическим анализом чувстви
-
тельности на каждой итерации проводится два расчета напряженно
-
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2004.
№
2
35


