В настоящее время разработаны алгоритмы оптимизации
,
позволя
-
ющие ослабить ограничения на число управляющих параметров в за
-
даче
.
В основе этих алгоритмов лежит рассматриваемая в настоящей
работе комбинация метода анализа чувствительности проекта
[4, 5]
к
изменению управляющих параметров и методов минимизации первого
или второго порядка точности
.
Напряж
e
нно
-
деформированное состояние диска определяется сле
-
дующей системой дифференциальных уравнений
[1, 2]:
du
dr
=
−
µ
r
u
+
1
−
µ
2
Er
1
h
Q
+
α
(1 +
µ
)
T,
dQ
dr
=
E
r
hu
+
µ
r
Q
+ (
−
EαT
−
ρω
2
r
2
)
h,
(1)
где
Q
=
σ
r
hr
;
r
—
радиус диска
;
σ
r
—
распределение радиальных на
-
пряжений по объему диска
;
u
—
перемещения точек диска
;
E
—
мо
-
дуль упругости материала диска
;
µ
—
коэффициент Пуассона
;
T
(
r
)
—
температура точек диска
;
ω
—
угловая частота вращения диска
;
ρ
—
плотность материала
;
α
—
коэффициент температурного расширения
;
h
(
r
)
—
толщины точек диска
.
Решение системы
(1)
получим для краевых условий общего вида
α
1
u
(
a
) +
β
1
Q
(
a
) =
η
1
,
α
2
u
(
b
) +
β
2
Q
(
b
) =
η
2
;
(2)
здесь
α
1
, α
2
, β
1
, β
2
—
некоторые коэффициенты
.
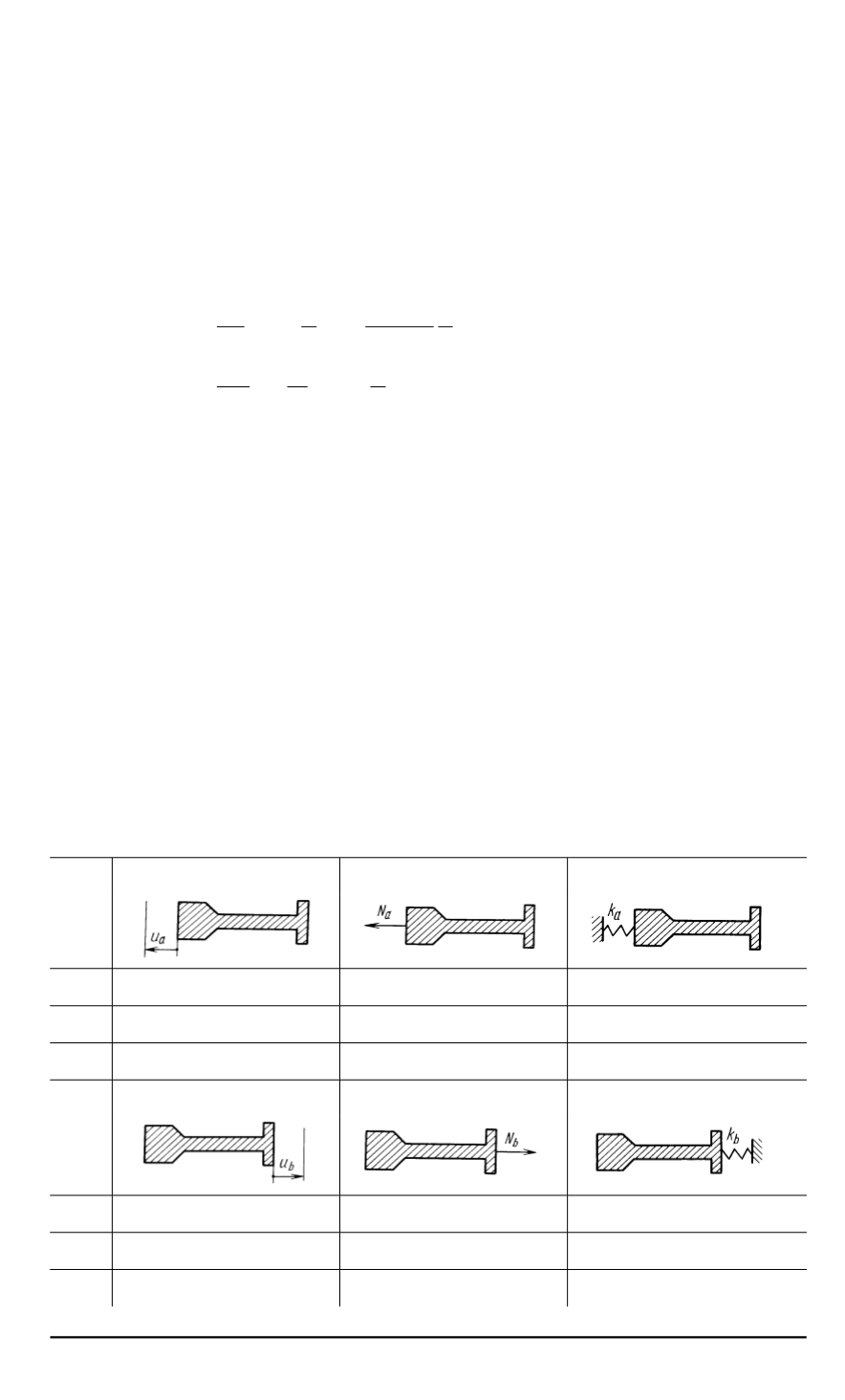
Линейные соотношения
(2)
определяют способы задания гранич
-
ных условий
,
приведенные в таблице
.
Заметим
,
что возможна комби
-
нация любого столбца для
r
=
a
с любым из столбцов для
r
=
b
.
Задано перемещение
Задана сила
Задана упругая связь
r
=
a
α
1
1
0
k
a
β
1
0
1
−
1
/a
η
1
u
a
N
a
a
0
Задано перемещение
Задана сила
Задана упругая связь
r
=
b
α
2
1
0
k
b
β
2
0
1
−
1
/b
η
2
u
b
N
b
b
0
24
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2004.
№
2


