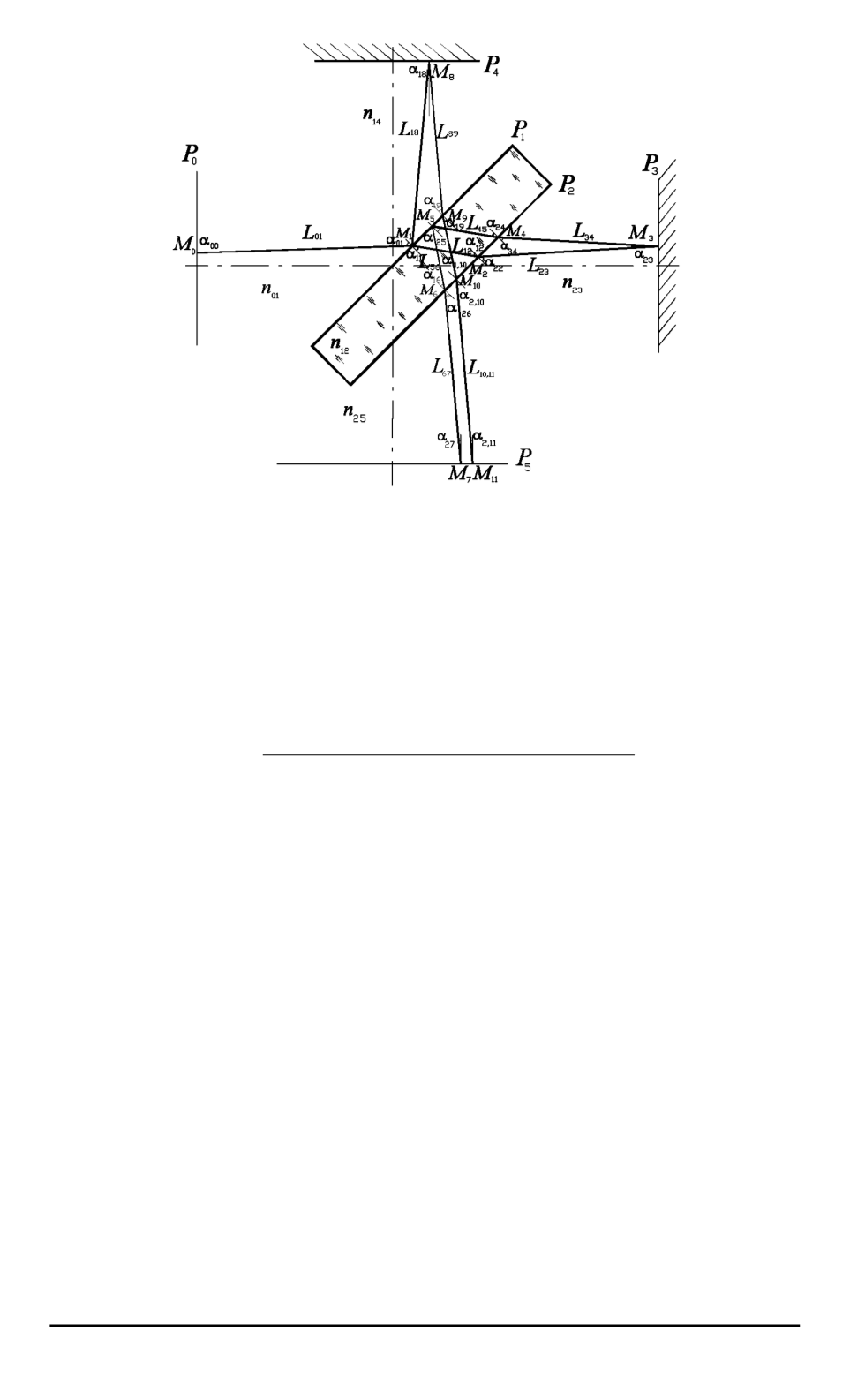
Рис
. 2.
Двумерная схема распространения лучей в интерферометре Майкельсо
-
на
(
в трехмерной модели рассматриваются
N
лучей
,
волновые векторы кото
-
рых направлены параллельно вектору
~a
i
−
1
,j
(
l
i
−
1
,j
, m
i
−
1
,j
, n
i
−
1
,j
)
;
каждый луч
характеризуется точкой
M
j
−
1
(
x
j
−
1
, y
j
−
1
, z
j
−
1
)
пересечения с поверхностью
P
i
)
E
2
(
t
) =
T
01
(
ω
0
)
E
0
(
t
−
t
01
−
t
12
)
×
×
exp(
−
i
(
ω
0
(
t
−
t
01
−
t
12
) +
ϕ
0
−
k
0
(
n
01
L
01
+
n
12
L
12
)));
(24)
здесь
t
12
=
n
12
L
12
/c
—
время распространения луча между поверхно
-
стями СД
,
L
12
=
p
(
x
2
−
x
1
)
2
+ (
y
2
−
y
1
)
2
+ (
z
2
−
z
1
)
2
;
сдвиг фазы
β
0
при прохождении через СД равен нулю
.
Введем величину
t
2
=
t
01
+
t
12
.
Тогда
E
2
(
t
) =
T
01
(
ω
0
)
E
0
(
t
−
t
2
)
×
×
exp(
−
i
(
ω
0
(
t
−
t
2
) +
ϕ
0
−
k
0
(
n
01
L
01
+
n
12
L
12
))
.
(25)
Затем электромагнитная волна падает на подвижное зеркало
—
плоскость
P
3
.
Амплитуда волны на подвижном зеркале равна
E
3
(
t
) =
T
01
(
ω
0
)
T
23
(
ω
0
)
E
0
(
t
−
t
3
) exp (
−
i
(
ω
0
(
t
−
t
3
) +
ϕ
0
−
−
k
0
(
n
01
L
01
+
n
12
L
12
+
n
23
(
L
23
+ ∆
L
23
(
t
)))))
,
(26)
где
t
3
=
t
01
+
t
12
+
t
23
+ ∆
t
3
;
∆
t
3
—
время распространения лу
-
ча между начальным и текущим положением подвижного зеркала
,
∆
t
3
=
n
23
∆
L
3
(
t
)
/c
;
∆
L
3
(
t
)
—
смещение зеркала в момент времени
t
;
t
23
=
n
23
L
23
/c
;
T
23
(
ω
0
)
—
амплитудный коэффициент пропускания
второй поверхности СД при прохождении луча в среду с показателем
преломления
n
23
для частоты
ω
0
.
32
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2004.
№
4


