μ
=
ητ/T
=
ηQ/
(
ω
0
T
)
:
Ψ (
μ
)
≈
Ξ
0
cos
ω
0
T
μ
ω
0
T
Q
Z
−∞
p
C
−
1
(
μ
)
C
0
dμ
+
α
0
C
−
1
(
μ
)
C
0
−
1
4
×
×
exp
−
1
2
ω
0
T
Q
μ
ω
0
T
Q
Z
−∞
C
−
1
(
μ
)
C
0
dμ
.
(21)
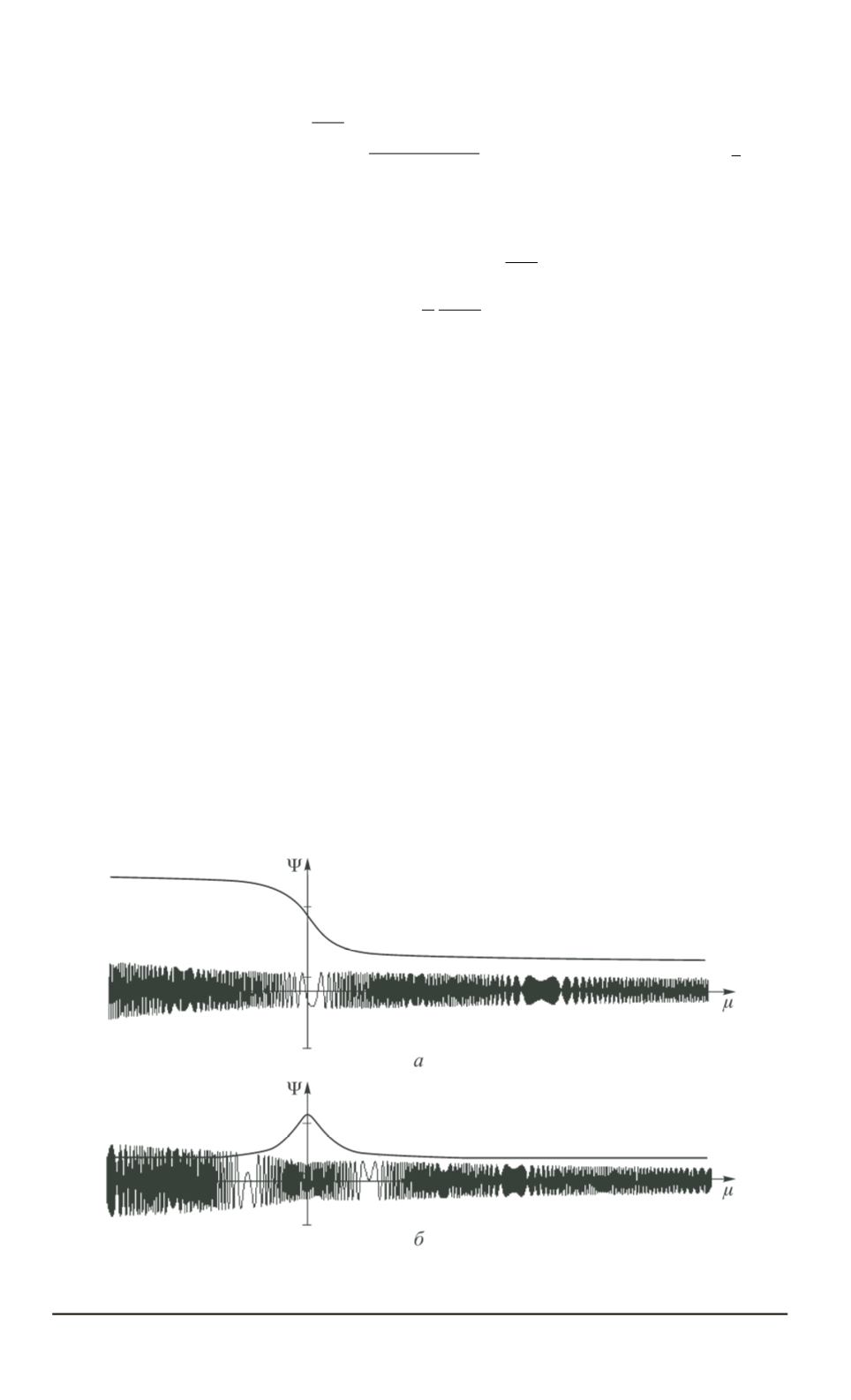
По формуле (21) проведен расчет, результаты которого представле-
ны на рис. 4.
Выводы.
Аналитически описаны характерные изменения емкости
(монотонно между двумя уровнями и при возврате к исходному уров-
ню), позволяющие корректно сформулировать задачи о двух типах
базовых переходных процессов как реакции на указанные выше изме-
нения.
Показано, что при анализе чисто реактивных ЭЦ с плавно изменя-
ющимися параметрами может быть использован гамильтонов форма-
лизм, что дает возможность приближенно описать переходные процес-
сы в терминах действие–фаза. Указана производящая функция, по ко-
торой выполнен переход к канонически сопряженным переменным для
цепей рассматриваемого класса. Для высокодобротной цепи в форме,
удобной для последующих асимптотически верных преобразований,
определено модельное уравнение. Это позволило найти приближение
Рис. 4. Переходной процесс
Ψ (
μ
)
в высокодобротной цепи при законах измене-
ния емкости типа плавного перепада (
а
) и плавного импульса (
б
)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 5
91


