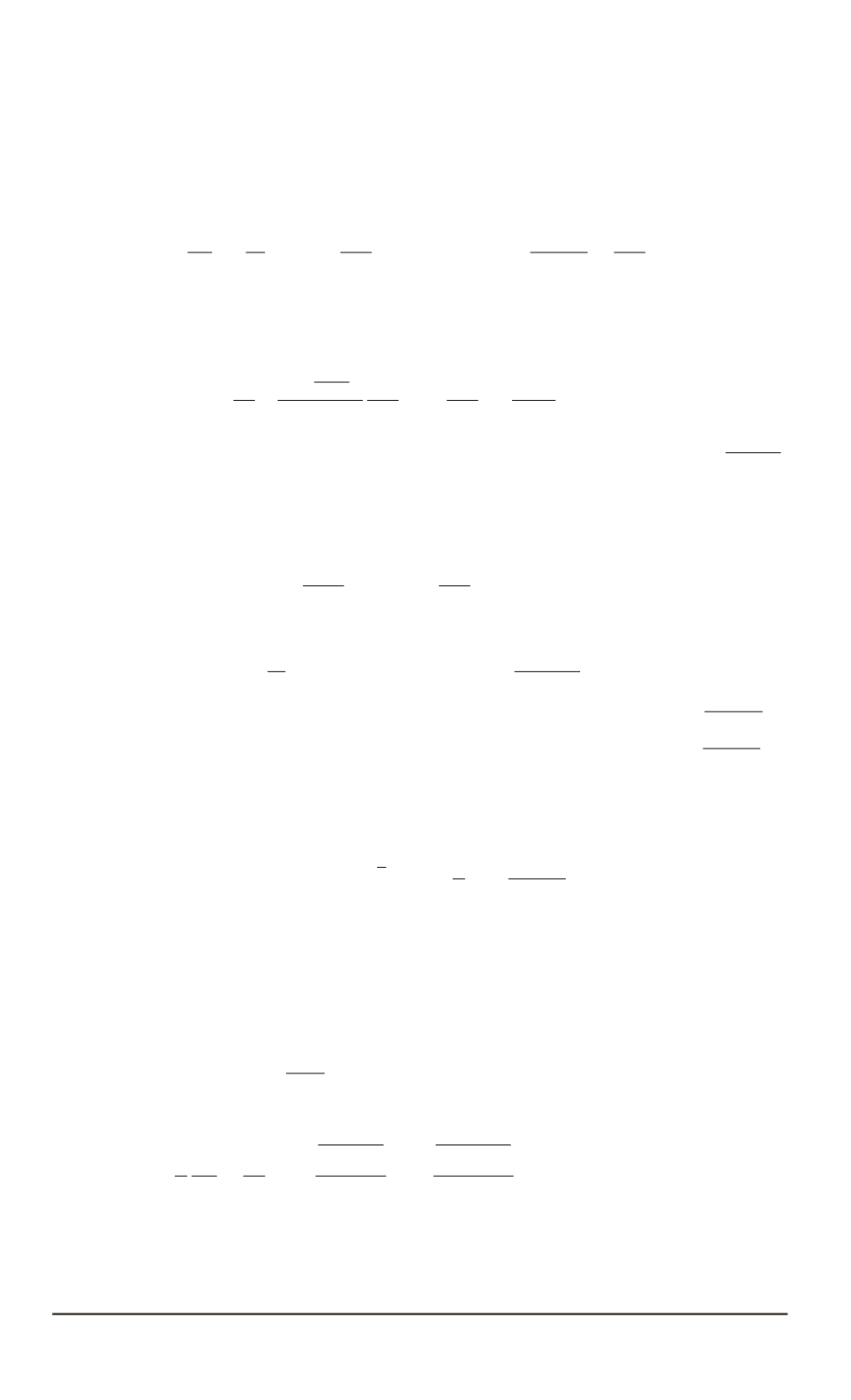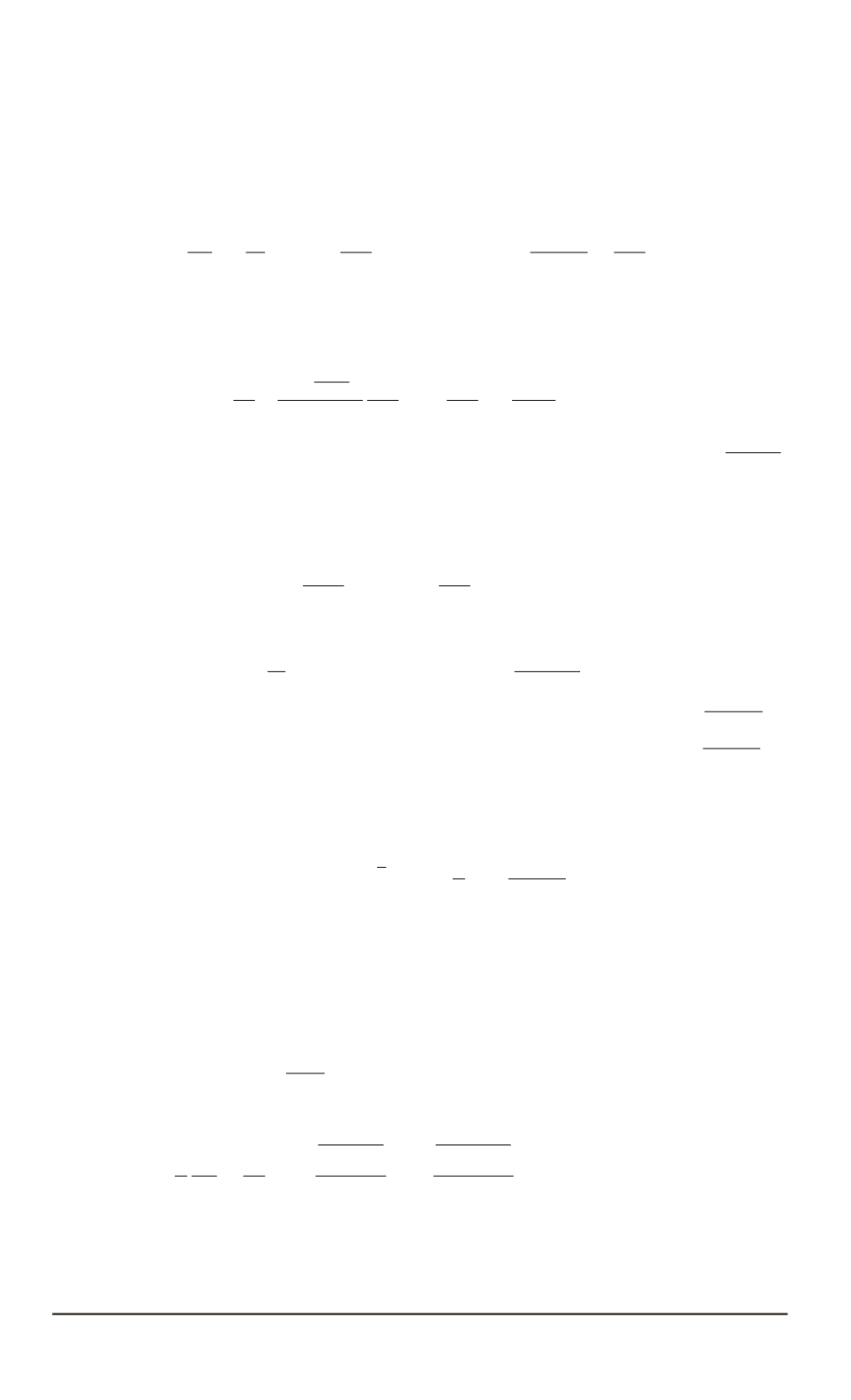
весия, т.е. фазовый объем сжимается (несправедлива теорема Лиувил-
ля). В этом случае гамильтониана не существует. Поэтому в качестве
модели выберем приведенное дифференциальное уравнение, которое
следует из очевидной системы уравнений для переменных состояния
(эти уравнения не приводятся к гамильтоновым):
dq
dt
+
Ψ
L
+
R
−
1
d
Ψ
dt
= 0;
q
=
C
t
−
t
0
T
d
Ψ
dt
.
Эта система сводится к уравнению второго порядка (уравнение не ла-
гранжева типа, но близко по форме к самосопряженному уравнению)
d
dt
"
C
t
−
t
0
T
C
0
d
Ψ
dt
#
+
d
Ψ
dt
+
Ψ
C
0
L
= 0
.
Введем следующие обозначения:
τ
=
C
0
R
;
η
= (
t
−
t
0
)
/τ
;
ρ
=
p
L/C
0
;
Q
=
R/ρ
1
— большая добротность. Тогда приведенное уравнение
примет вид
f
2
(
η
)
d
2
Ψ
d
2
η
+
f
1
(
η
)
d
Ψ
dη
+
Q
2
Ψ = 0
,
(16)
где
f
2
(
η
) =
h
C
−
1
η
τ
T
C
0
i
−
1
;
f
1
(
η
) = 1 +
df
2
(
η
)
dη
.
В (16) введем новую независимую переменную
ζ
(
η
) =
η
Z
−∞
s
1
f
2
(
η
)
dη
и новую функцию
Ξ (
ζ
) = Φ (
η
) Ψ (
η
)
, где
Φ (
η
) =
f
2
(
η
)
−
1
4
exp
1
2
η
Z
−∞
f
1
(
η
)
f
2
(
η
)
dη
.
(17)
Преобразование независимой переменной и искомой функции,
представленной выше, есть преобразование Лиувилля [8]. Оно приво-
дит уравнение (16) к нормальной форме Лиувилля [8]:
d
2
Ξ
dζ
2
+
Q
2
+
ϕ
(
ζ
) Ξ = 0
,
(18)
где
ϕ
(
ζ
) =
1
2
d
dζ
1
f
2
f
2
2
d
Φ (
η
)
dζ
Φ (
η
)
−
f
2
d
2
Φ (
η
)
dζ
2
Φ (
η
)
— функция, ограниченная
по модулю малой величиной, поскольку зависит только от производ-
ных плавно меняющихся функций
Φ (
η
)
по безразмерному времени и
не зависит от максимумов модулей последних. Это можно показать,
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 5
89