Равенства (12) можно получить более корректно, усредняя (11) и
(12) по “быстрой” фазе
θ
и полагая плавно изменяющуюся емкость
постоянной. Асимптотически постоянное действие
I
называют адиа-
батическим инвариантом этой задачи. В цепи с потерями такого инва-
рианта уже не существует.
Получив асимптотически пригодные (приближенные) действие и
фазу, можно вернуться к исходным переменным в силу (5) и (6):
q
(
η
) =
ρ
−
1
s
2
I
0
√
C
−
1
C
0
sin
p
C
−
1
C
0
η
+
θ
0
;
(13)
Ψ (
η
) =
q
2
I
0
p
C
−
1
C
0
cos
p
C
−
1
C
0
η
+
θ
0
.
(14)
Чтобы найти переходной процесс, необходимо в уравнениях (13) и
(14) перейти к заданным начальным условиям при
t
=
−∞
. Нетрудно
показать, что
2
I
0
=
p
C
−
1
(
−∞
)
C
0
ρ
2
q
2
0
+
p
C
−
1
(
−∞
)
C
0
−
1
Ψ
2
0
;
θ
0
=
= arcctg
p
C
−
1
(
−∞
)
C
0
ρq
0
Ψ
0
.
(15)
Выражения (13)–(15) совместно с базовыми законами изменения
емкости дают возможность построить переходные процессы на ком-
пьютере (рис. 3).
Переходные процессы в высокодобротной цепи.
Цепь с потеря-
ми, возбуждаемая параметрически, гамильтоновой системой не явля-
ется. Переходной процесс стремится к устойчивому состоянию равно-
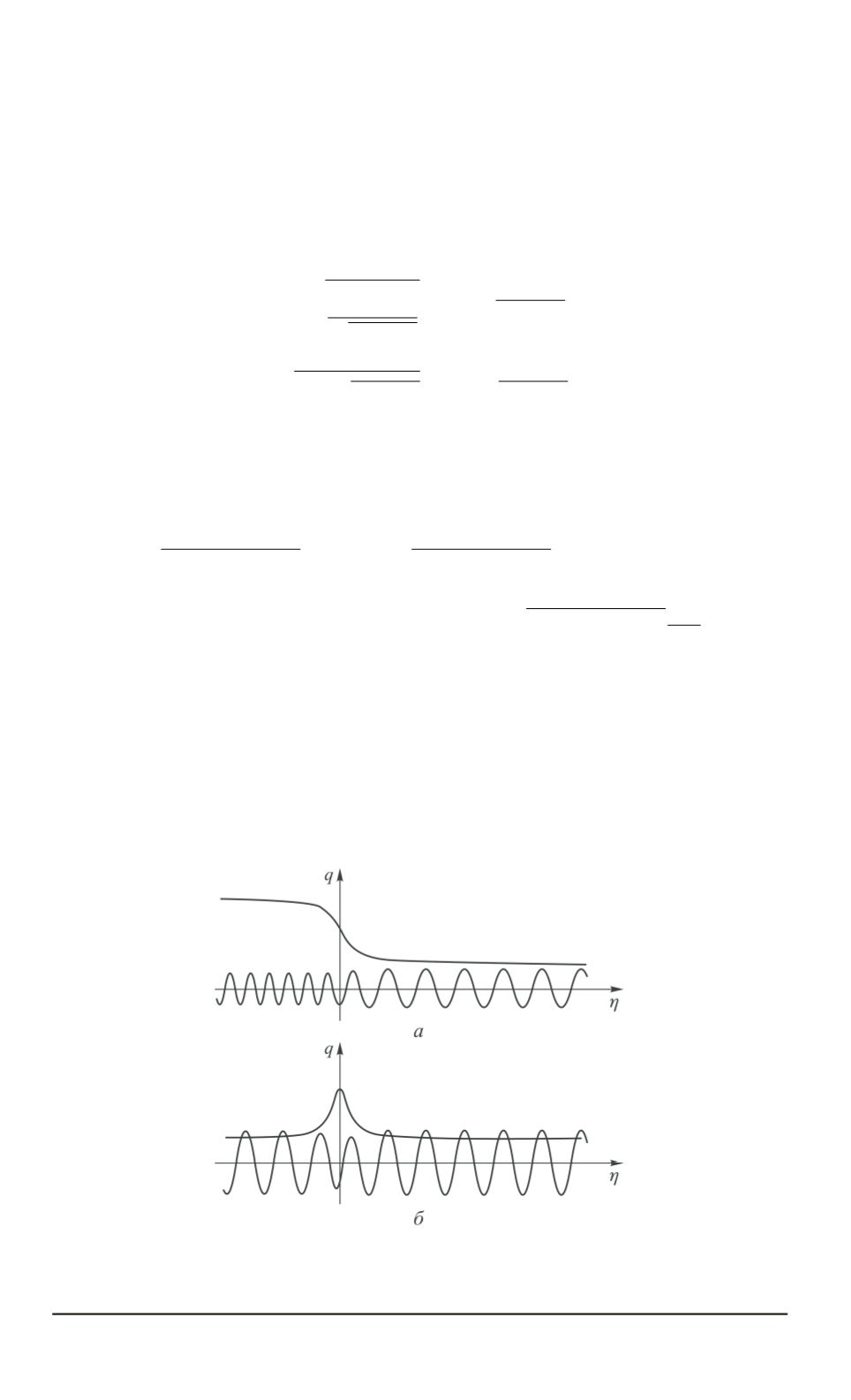
Рис. 3. Переходной процесс
q
(
η
)
в чисто реактивной цепи при законах
изменения емкости типа плавного перепада (
а
) и плавного импульса (
б
)
88
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 5


