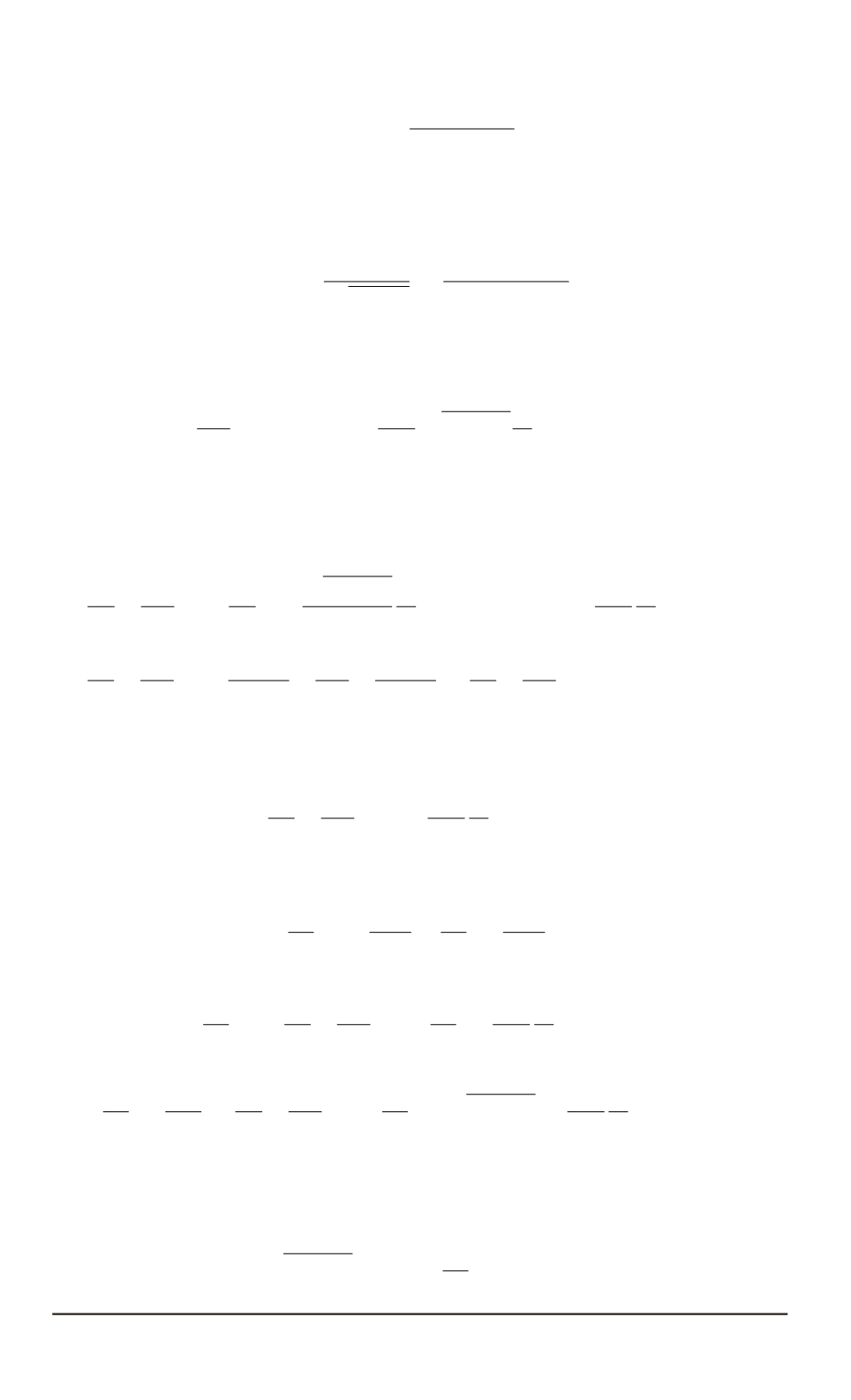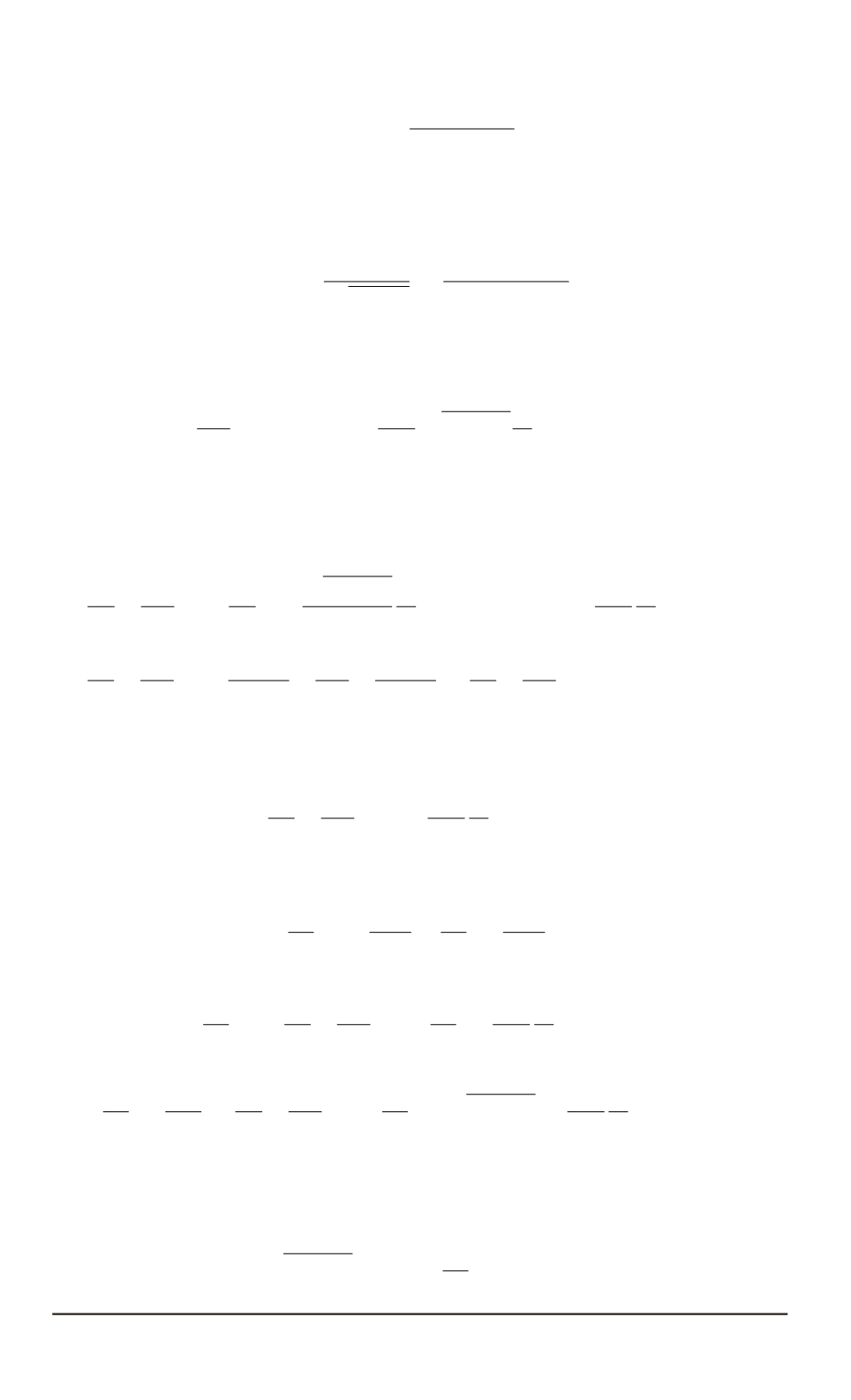
В новых переменных с использованием (5) и (6) гамильтониан (1)
преобразуется к виду
H
=
I
q
C
(
t
)
−
1
C
0
.
Однако гамильтониан после канонического преобразования отличает-
ся от приведенного выше гамильтониана
H
:
H
0
=
I
p
CC
−
1
0
+
∂F
(
ρq, θ, η
)
∂η
.
(7)
При вычислении производной следует учитывать, что берется частная
производная времени
η
:
∂F
∂η
(
ρq, θ, η
) =
−
1
4
ω
0
p
C
−
1
C
0
˙
C
C
(
ρq
)
2
ctg
θ.
(8)
В (8) точка обозначает производную емкости
С
по времени
t
.
Для получения гамильтоновых уравнений из нового гамильтониана
(7) необходимо знать частные производные:
∂
∂I
∂F
∂η
=
∂
∂I
−
√
C
−
1
C
0
4
ω
0
˙
C
C
(
ρq
)
2
ctg
θ
!
=
−
1
4
ω
0
˙
C
C
sin 2
θ
;
∂
∂θ
∂F
∂η
=
∂
∂
(
ρq
)
∂F
∂η
∂
(
ρq
)
∂θ
+
∂
∂θ
∂F
∂η
.
(9)
Опуская в последнем выражении из (9) промежуточные вычисле-
ния, получаем
∂
∂θ
∂F
∂η
=
−
1
2
ω
0
˙
C
C
I
cos 2
θ.
Гамильтоновы уравнения для канонических переменных в общем виде
dI
dη
=
−
∂H
0
∂θ
;
dθ
dη
=
∂H
0
∂I
,
или
dI
dη
=
−
∂
∂θ
∂F
dη
→
dI
dη
=
1
2
ω
0
˙
C
C
I
cos 2
θ
;
(10)
dθ
dη
=
∂H
∂I
+
∂
∂I
∂F
dη
→
dθ
dη
=
p
C
−
1
C
0
−
1
4
ω
0
˙
C
C
sin 2
θ.
(11)
Из (10) и (11) следует, что с точностью до малого отношения
˙
C/
(
ω
0
C
) 1
(эквивалентно
ω
0
T
1
) существуют равенства
θ
(
η
)
≈
p
C
−
1
C
0
η
+
θ
0
;
dI
dη
≈
0
→
I
(
η
)
≈
I
0
.
(12)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 5
87