
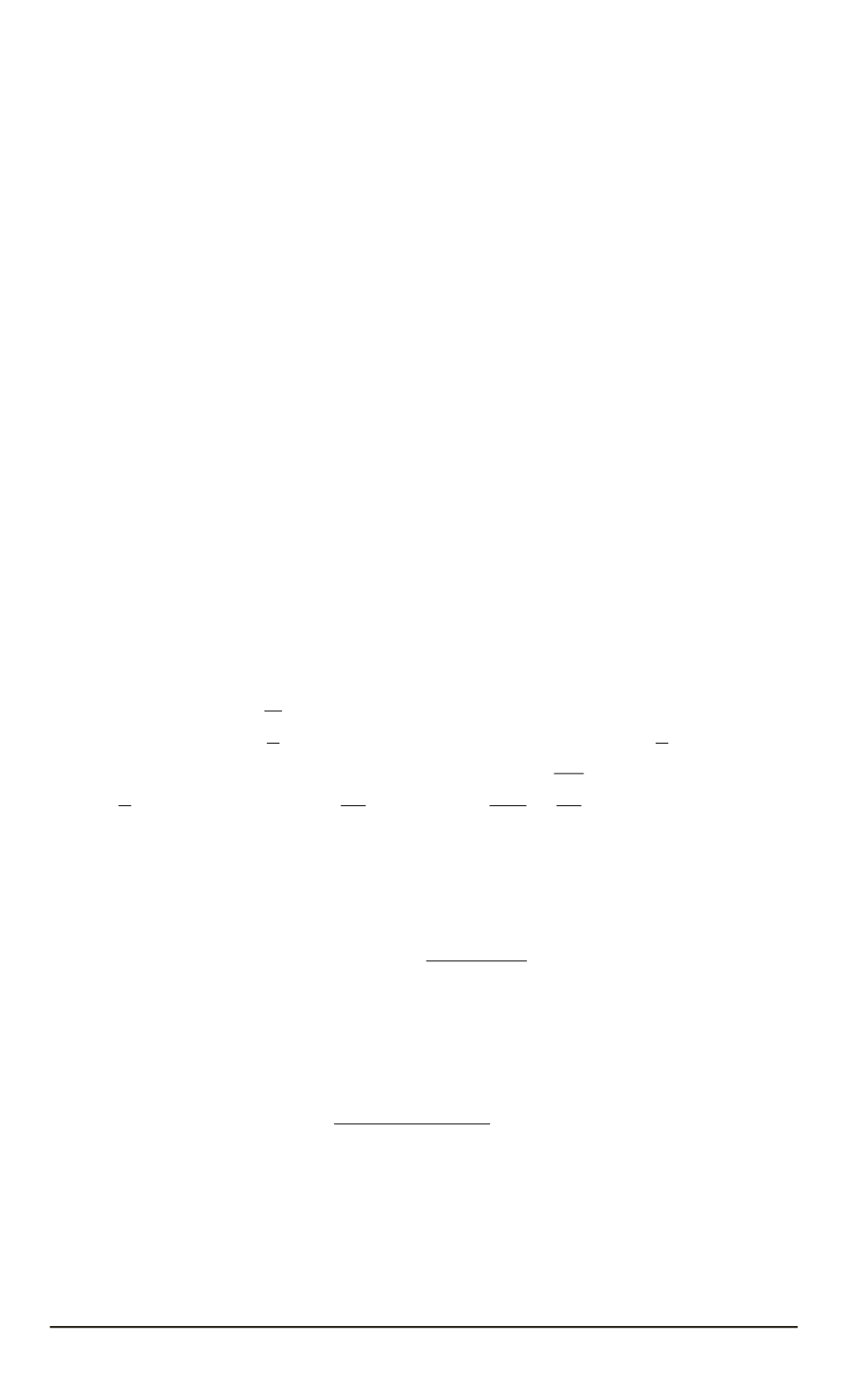
После выполнения соответствующих операций имеем
∞
X
n
=0
C
n
(
n
/2 +
ρ
) (
n
/2 +
ρ
−
1) (
x
∗
−
x
)
n
/2+
ρ
−
2
=
=
∞
X
n
=0
D
∗∗
n
(
x
∗
−
x
)
n
/2+5
ρ
+
∞
X
n
=0
B
n
(
x
∗
−
x
)
n
,
(7)
где
D
∗∗
n
=
n
X
i
=0
D
∗
n
−
i
C
i
,
D
∗
n
=
n
P
i
=0
D
n
−
i
D
i
,
D
n
=
n
P
i
=0
C
n
−
i
C
i
,
n
= 0
,
1
,
2
, . . .
Равенство (7) обратится в тождество при выполнении условий
1)
n
/2 +
ρ
−
2 =
n
/2 + 5
ρ
;
(8)
2)
C
n
(
n
/2 +
ρ
) (
n
/2 +
ρ
−
1) =
D
∗∗
n
.
(9)
Здесь
D
∗∗
n
=
D
∗∗
n
, n
∈ {
0
,
1
,
2
,
3
,
4
,
6
,
8
, ...,
2
k
}
;
D
∗∗
n
+
B
n
−
5
, n
∈ {
5
,
7
,
9
, ...,
2
k
+ 1
}
.
(10)
Из условия (8) следует
ρ
=
−
1
/
2
, а соотношение (9) позволяет од-
нозначно определить все коэффициенты
C
n
. При этом вариант
C
0
= 0
отбрасываем, так как в этом случае получаем противоречие с предпо-
ложением относительно характера особой точки
x
∗
. Согласно соотно-
шению (9),
C
0
=
4
r
3
4
,
C
1
=
C
2
=
C
3
=
C
4
= 0
,
C
5
=
−
4
7
B
0
,
C
6
=
α
,
C
7
=
4
9
B
1
,
C
8
= 0
,
C
9
=
4
33
B
2
,
C
10
=
20
147
4
r
27
4
B
2
0
. Таким образом,
получено однозначно формальное представление решения задачи (2),
(3) в окрестности точки
x
∗
в виде (4).
Докажем сходимость правильной части ряда (4) в области (5). Из
условия теоремы следует
M
= sup
n
r
(
n
)
(
x
∗
)
n
!
,
n
= 0
,
1
,
2
, . . .
, тогда для
коэффициентов ряда (6) справедлива оценка
|
B
n
| ≤
M.
(11)
Из выражения (9) с учетом (10), (11) для коэффициентов
C
n
пред-
полагаем оценку:
|
C
n
| ≤
1
(
n
+ 2) (
n
−
6)
2
n
M
(
M
+ 1)
[
n
/5]
=
v
n
,
n
=
= 0
,
1
,
2
, . . .
Исходя из закономерности образования коэффициентов
C
n
, с помощью метода математической индукции докажем эту оценку
для коэффициента
C
n
+1
при
n
+ 1 = 5 (2
k
+ 1) = 10
k
+ 5
:
|
C
10
k
+5
((10
k
+ 5) /2 +
ρ
) ((10
k
+ 5) /2 +
ρ
−
1)
| ≤
≤
D
∗∗
10
k
+5
≤
D
∗∗
10
k
+5
+
B
10
k
≤
D
∗∗
10
k
+5
+
|
B
10
k
| ≤
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 2
29

















