
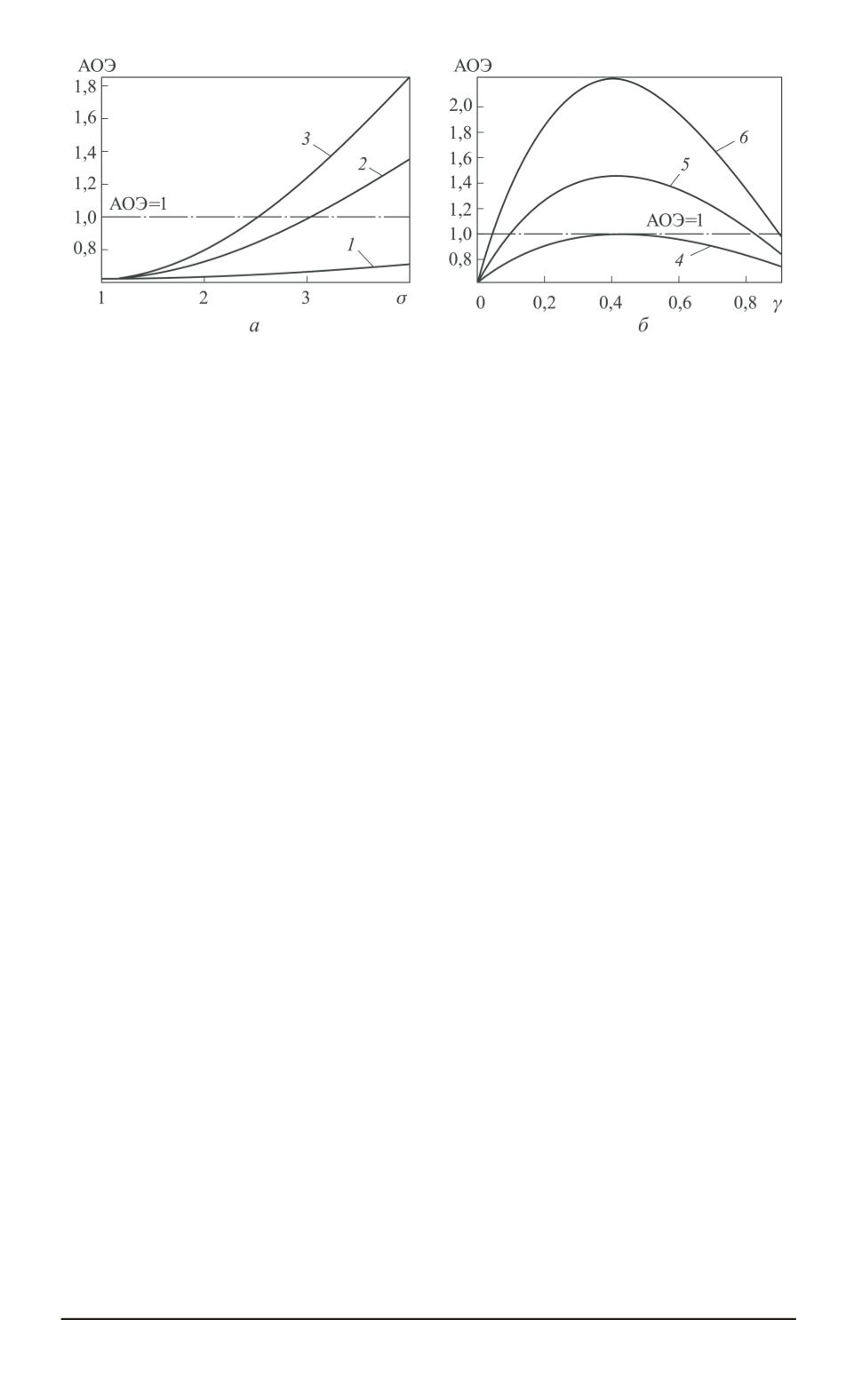
Зависимости АОЭ от величины
σ
(
а
) при
γ
= 0
,
01
(
1
), 0,1 (
2
), 0,2 (
3
) и от
величины
γ
(
б
) при
σ
= 2
,
22
(
4
), 3,0 (
5
), 4,0 (
6
)
величины с дисперсией
τ
, а не
σ
, этих засорений с увеличением пара-
метра
γ
становится все меньше и меньше. Именно этим объясняется
падение эффективности при
γ >
0
,
5
. На практике значение
γ
обычно
не превышает 0,15.
Заключение.
В работе изложен метод вычисления АОЭ оцен-
ки наименьших модулей по отношению к оценке максимального
правдоподобия для параметра авторегрессионного уравнения первого
порядка со случайным коэффициентом. Установлено, что если пред-
положения о распределении обновляющего поля выполняются лишь
приближенно, то оценка максимального правдоподобия уступает в
эффективности оценке наименьших модулей.
ЛИТЕРАТУРА
1.
Nicholls D.F.
,
Quinn B.G.
Random coefficient autoregressive models: an introduction.
N.Y.–Berlin: Springer-Verlag, 1982. 154 p.
2.
Tong H.
Nonlinear time series. A dynamical system approach. N.Y.: Clarendon Press,
1990. 564 p.
3.
Diaconis P.
,
Freedman D.
Iterated random functions // SIAM Rev. 1999. Vol. 41.
No. 1. P. 45–76.
4.
Aue A.
,
Horv´ath L.
,
Steinebach J.
Estimation in random coefficient autoregressive
models // J. Time Ser. Anal. 2006. Vol. 27. No. 1. P. 61–76.
5.
Truquet L.
,
Yao J.
On the quasi-likelihood estimation for random coefficient
autoregressions // Statistics. 2012. Vol. 46. No. 4. P. 505–521.
6.
Робастность
в статистике. Подход на основе функций влияния / Ф. Хампель,
Э. Рончетти, П. Рауссеу, В. Штаэль; пер. с англ. М.: Мир, 1989. 512 с.
REFERENCES
[1] Nicholls D.F., Quinn B.G. Random coefficient autoregressive models: an
introduction. N.Y.–Berlin, Springer-Verlag, 1982. 154 p.
[2] Tong H. Nonlinear time series. A dynamical system approach. New York, Clarendon
Press, 1990, 564 p.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 3
29

















