
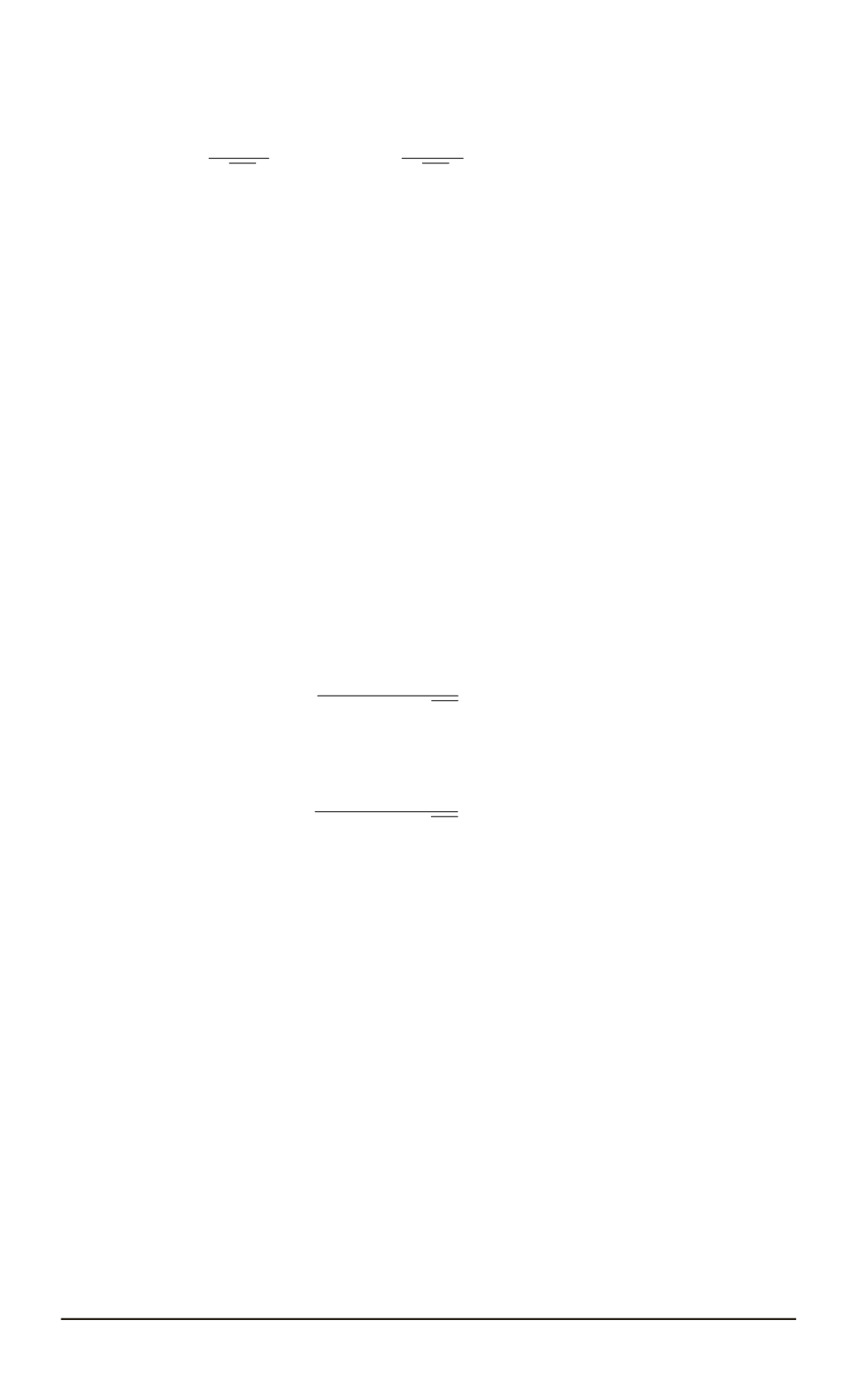
случайных величин. Хорошей моделью нарушения предположений о
нормальности является распределение Тьюки (см. [6]) с плотностью
f
(
x
) = (1
−
γ
)
1
√
2
πτ
e
−
x
2
/
(2
τ
2
)
+
γ
1
√
2
πσ
e
−
x
2
/
(2
σ
2
)
,
0
≤
γ
≤
1
, τ >
1
.
Последовательность случайных величин, имеющих распределение
Тьюки, имитирует типичное на практике загрязнение последователь-
ности нормальных величин с нулевым математическим ожиданием и
дисперсией
τ
2
, добавляя в нее случайно с вероятностью
γ
нормальные
случайные величины также с нулевым математическим ожиданием,
но с большей, чем
τ
2
, дисперсией
σ
2
.
Если величины
η
1
имеют усеченное нормальное распределение, а
ε
1
— распределение Тьюки, то
E
ε
n
1
=
(
0
,
если
n
нечетно
;
(
n
−
1)!!((1
−
γ
)
τ
n
+
γσ
n
,
если
n
четно
.
Следовательно, ряд (7) будет расходиться. Поэтому предположим, что
величины
ε
1
имеют усеченное распределение Тьюки:
f
ε
(
x
) = (1
−
γ
)
g
1
(
x
) +
γg
2
(
x
)
,
где
g
1
(
x
) =
e
−
x
2
/
(2
τ
2
)
2Φ
0
(
k
τ
)
τ
√
2
π
,
если
|
x
| ≤
k
τ
τ
;
0
,
если
|
x
| ≤
k
τ
τ,
g
2
(
x
) =
e
−
x
2
/
(2
σ
2
)
2Φ
0
(
k
σ
)
σ
√
2
π
,
если
|
x
| ≤
k
σ
σ
;
0
,
если
|
x
| ≤
k
σ
σ,
k
τ
,
τ
,
k
σ
,
σ
— некоторые положительные постоянные. Вычисляя АОЭ
по формуле (6), получаем, что она не только превышает в ряде слу-
чаев единицу, но и может быть сколь угодно большой с возрастанием
доли загрязнения
γ
и уровня загрязнения
σ
. Изложенное хорошо ил-
люстрируют зависимости АОЭ от величин
γ
и
σ
. Для определенности
предполагалось, что
ϕ
= 0
,
1
,
ω
= 0
,
01
,
k
ω
= 3
,
k
τ
= 3
,
τ
= 1
,
k
σ
= 3
.
Зависимость АОЭ от величины
σ
при различных значениях
γ
при-
ведена на части
а
рисунка, а зависимость АОЭ от величины
γ
при
различных значениях
σ
— на части
б
рисунка. Видно, что с возраста-
нием величин
γ
и
σ
АОЭ увеличивается, становясь при
σ >
2
,
22
для
некоторых значений
γ
больше единицы, что свидетельствует о пре-
восходстве для этих значений параметров
γ
и
σ
оценки наименьших
модулей над оценкой максимального правдоподобия. Отметим, что
при
γ >
0
,
5
роль засорения наблюдений начинают играть случайные
28
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 3

















