Осесимметричная смешанная задача для составного пространства с монетообразной трещиной

11 / 16

+
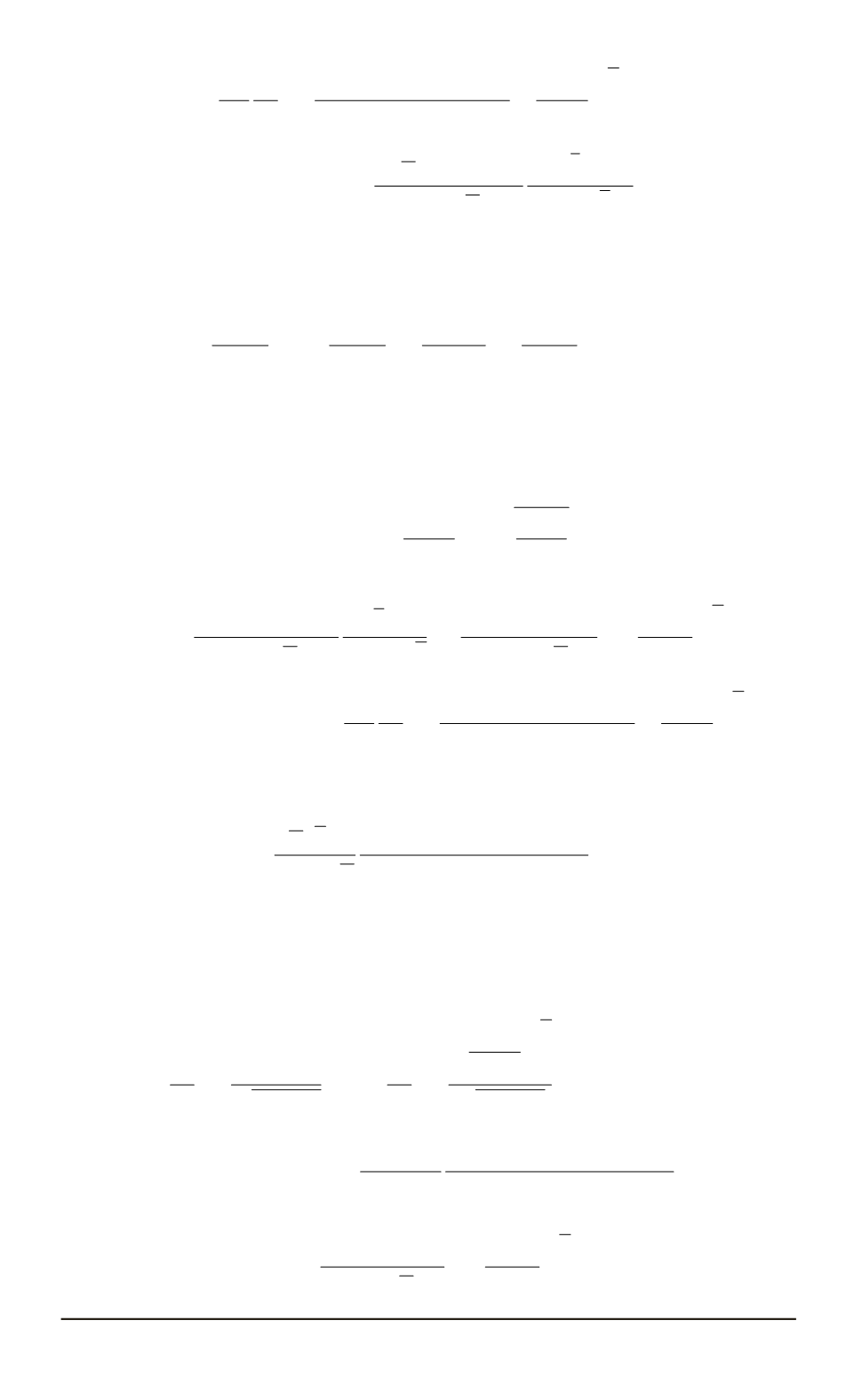
D2
r
d
dr
a Z0
tψ (t, r) − aψ (a, r)
r − t
t
a − t
γ
dt =
=
πaγψ (a, r) D2
sin πγ
rγ−1
(r − a)γ+1 + ϕ1 (r) . (22)
Отметим, что при получении формулы (22) было использовано значе-
ние интеграла [11]
b Za
x − a
b − x
α−1 dx
x − y
=
π
sin απ
a − y
b − y
α− 1
− 1! ,
0 < Reα < 2; y < a < b; y > b > a,
и введены обозначения
ψ (t, r ) =
a + t
t
γ r r − t
r + t
;
ϕ1 (r) = −
aπ ˉγD2ψ (a, r)
sin πγ
rγ−2
(r − a)γ −
aπD2ψ0 (a, r)
r sin πγ " r
r − a
γ
− 1# +
+
D 2
r
d
dr
a Z0
tψ (t, r) − aψ (a, r)
r − t
t
a − t
γ
dt.
Подставляя в (22) значение функции ψ (t, r) в точке a, получаем
I1 (r) = −
πγ2γ D2
a sin πγ
(r/a )ˉ γ−1 (r/a + 1)−1/2
(r/a − 1)1/2+ˉγ
+ ϕ1 ( r) .
Нетрудно проверить, что особенность функции ϕ1 (r) в точке r = a
более низкого порядка, чем особенность первого слагаемого.
Аналогично определим функции
I2 (r) =
d
dr
a Z0
ϕ2 ( t) dt
√r2 − t2
= D2
d
dr
a Z0
a + t
a − t
γ
√ r2 − t2
dt =
=
πˉγ2ˉ γ D2
a sin πˉγ
(r/a )ˉ γ−1 (r/a + 1)− 1/2
(r/a − 1)1/2+ˉγ + ϕ2 (r) ;
ϕ 2 ( r) = −
πD2ψ0 (a, r)
sin πγ " r
r − a
γ
− 1# +
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 3 41