
полупространств одинаковые
(
ν
1
=
ν
2
=
ν
)
. Результаты расчетов при-
ведены в табл. 1, 2.
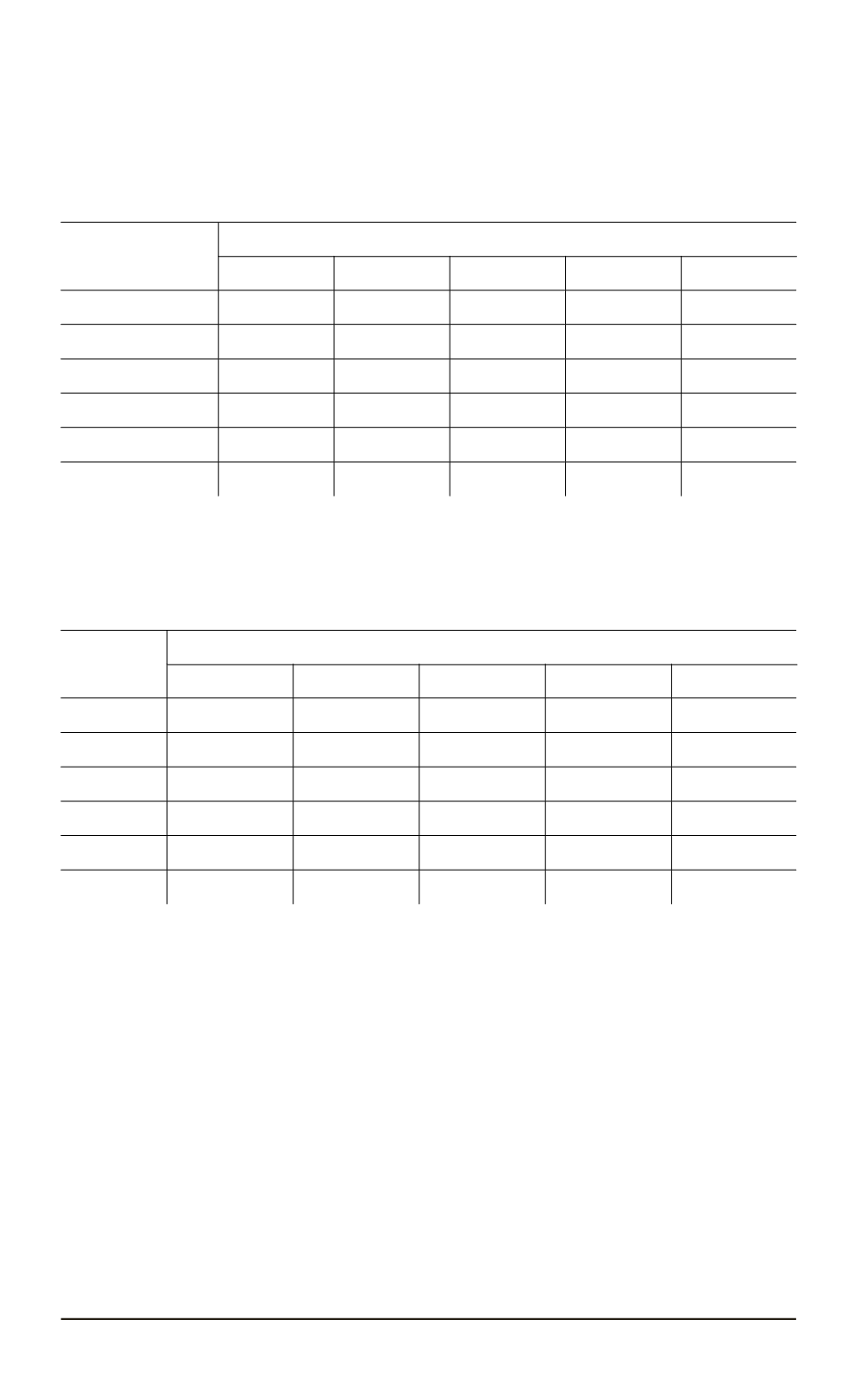
Таблица 1
Значения жесткого смещения
δ
∗
в зависимости от значений
коэффициентов
μ
и
ν
Значения
μ
Значения
ν
0,1
0,2
0,3
0,4
0,45
0,2
0,2329
0,2097
0,1693
0,1043
0,0585
0,6
0,1846
0,1684
0,1379
0,0860
0,0484
1,0
0,1590
0,1453
0,1192
0,0744
0,0419
1,5
0,1387
0,1266
0,1037
0,0647
0,0364
5,0
0,0847
0,0764
0,0618
0,0381
0,0214
10
0,0608
0,0544
0,0437
0,0268
0,0150
Таблица 2
Значения коэффициентов интенсивности
K
∗
I
(числитель) и
K
∗
II
(знаменатель)
в зависимости от значений коэффициентов
μ
и
ν
Значения
μ
Значения
ν
0,1
0,2
0,3
0,4
0,45
0,2 0,0243/0,0114 0,0278/0,0106 0,0323/0,0090 0,0381/0,0060 0,0417/0,0035
0,6 0,0307/0,0173 0,0360/0,0164 0,0428/0,0142 0,0516/0,0096 0,0570/0,0057
1,0 0,0323/0,0182 0,0380/0,0173 0,0453/0,0151 0,0548/0,0103 0,0605/0,0061
1,5 0,0328/0,0177 0,0384/0,0168 0,0456/0,0146 0,0549/0,0099 0,0606/0,0059
5,0 0,0291/0,0113 0,0331/0,0105 0,0382/0,0089 0,0449/0,0059 0,0490/0,0035
10 0,0243/0,0072 0,0271/0,0065 0,0308/0,0054 0,0357/0,0035 0,0389/0,0021
Данные, представленные в табл. 1, 2, показывают, что жесткие сме-
щения убывают, а коэффициенты интенсивности по абсолютной вели-
чине сначала возрастают, а затем убывают, когда жесткость нижне-
го полупространства постоянна, а жесткость верхнего полупростран-
ства возрастает при постоянном значении коэффициента Пуассона.
При постоянном значении отношения жесткостей полупространств
(
μ
=
const) жесткое смещение штампа и коэффициент
K
∗
II
умень-
шаются, а коэффициент
K
∗
I
увеличивается.
ЛИТЕРАТУРА
1.
Мусхелишвили Н.И.
Некоторые основные задачи математической теории упру-
гости. М.: Наука, 1966. 504 с.
44
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 3

















